


Next: 3.5 Boundary and Interface
Up: 3. Diffusion Phenomena in
Previous: 3.3 Equilibrium Diffusion
Subsections
After implantation substitional dopant atoms are immobile.
The dopant diffusion process is only possible when substitional dopant atoms interact with native point defects by building dopant-point defect pairs.
Silicon point defects are temporarily consumed to generate mobile species (dopant-point defect pairs), which then migrate into the silicon wafer interior, where the mobile dopants settle down on lattice sites to become a substitutional dopants, releasing silicon point defects in the process [25,24,26,20].
In the cases where a strong source of point defects exists on the wafer surface, transport of the dopant-point defects pairs causes a supersaturation of the point defects in the bulk region, and subsequentially kinks and ledges of the dopant profiles become apperant.
The tails of dopant profiles diffuse much faster than expected, which is exactelly what is observed experimentally [29,26,27,30].
Due to the active participation in the dopant diffusion, native silicon point defects exhibit dynamics which significantelly depart from the equilibrium state [21,6].
In the following sections three widely applied non-equilibrium models for the point defect assisted dopant diffusion are presented.
The simplest way to model the impact of the non-equilibrium interstitials' and vacancies' dynamic is using the cumulative diffusion coefficient,
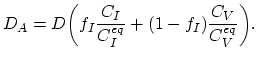 |
(3.39) |
Here,
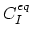 and
and
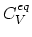 are equilibrium values of interstitial and vacancy concentrations, respectively.
The parameter
are equilibrium values of interstitial and vacancy concentrations, respectively.
The parameter 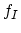 takes the value of one, if the diffusion works exclusively via interstitials, and zero if it works exclusively via vacancies.
takes the value of one, if the diffusion works exclusively via interstitials, and zero if it works exclusively via vacancies.
The model assumes that the dopant-defect pairing reactions and pair dissociation/defect recombination are in local equilibrium.
The recombination and generation of Frankel pairs are modeled by,
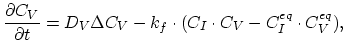 |
(3.40) |
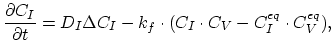 |
(3.41) |
denoting the reaction constant as 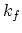 , and the diffusion coefficient of interstitials and vacancies as
, and the diffusion coefficient of interstitials and vacancies as 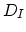 and
and 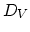 , respectively. Taking the diffusion coefficient
, respectively. Taking the diffusion coefficient 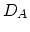 as defined by (3.39) the dopant diffusion is modeled by a simple diffusion equation,
as defined by (3.39) the dopant diffusion is modeled by a simple diffusion equation,
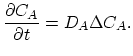 |
(3.42) |
This model is correct in the case of enhanced and oxidation retarded diffusion for low concentrations of dopants [20].
3.4.2 Three-Stream Mulvaney-Richardson Model
Under most annealing conditions, with exception of the rapid thermal annealing (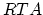 ), the dopant-defect pairing reactions are fast enough to maintain the pair concentration near local equilibrium with the concentrations of isolated dopands and defects,
), the dopant-defect pairing reactions are fast enough to maintain the pair concentration near local equilibrium with the concentrations of isolated dopands and defects,
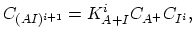 |
(3.43) |
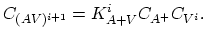 |
(3.44) |
Further simplifications is to aggregate different charge states of the species taking part in reactions to one single concentration. The last step was done in [29] in order to obtain model described by following equations,
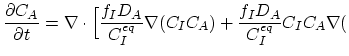 ln ln![$\displaystyle n)\Bigr] +$](img350.png) |
|
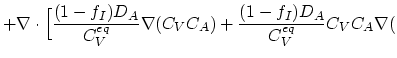 ln ln![$\displaystyle n)\Bigr],$](img352.png) |
(3.45) |
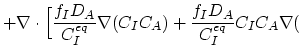 ln ln![$\displaystyle n)\Bigr],$](img352.png) |
(3.46) |
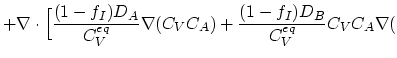 ln ln![$\displaystyle n)\Bigr].$](img357.png) |
(3.47) |
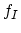 is the fractional contribution of the interstitial mechanism to the dopants diffusion.
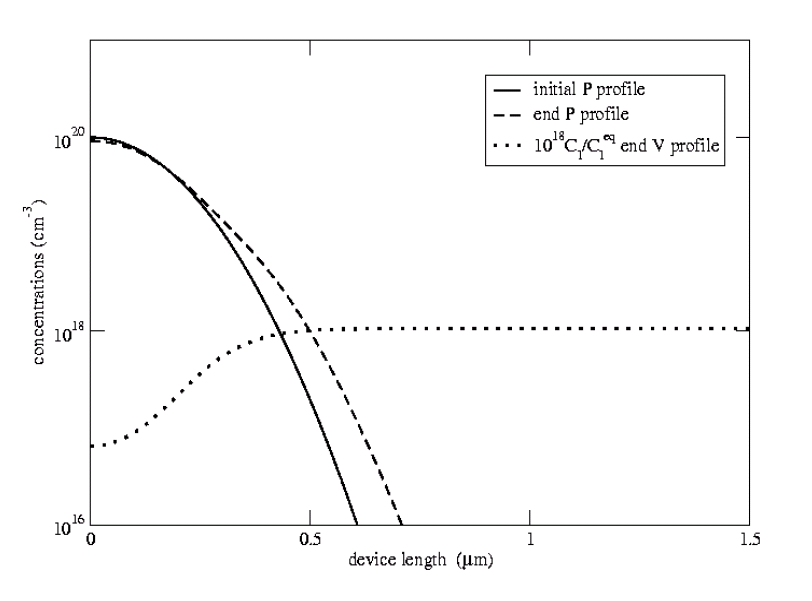
The approach of Mulvaney and Richardson [29] successfully models kink and tail diffusion of boron and phosphorus (Figure 3.1).
is the fractional contribution of the interstitial mechanism to the dopants diffusion.
The approach of Mulvaney and Richardson [29] successfully models kink and tail diffusion of boron and phosphorus (Figure 3.1).
Figure 3.1:
Diffusion of phosphorus at
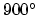 C for one hour. Phosphorus
diffuses primarily through pairing with intrinsic
interstitials. The nonequlibrium dynamics of the intrinsic
interstitials accounts for characteristic kink and tail parts of the final profile.
C for one hour. Phosphorus
diffuses primarily through pairing with intrinsic
interstitials. The nonequlibrium dynamics of the intrinsic
interstitials accounts for characteristic kink and tail parts of the final profile.
|
|
Taking into account non-equilibrium reactions of dopants and point defects we have to deal with a system of five equations (five-stream model).
These are continuity equations for the total concentrations of A , AI, AV, I, V, over all charge states for each species [30],
, AI, AV, I, V, over all charge states for each species [30],
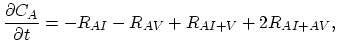 |
(3.48) |
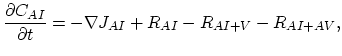 |
(3.49) |
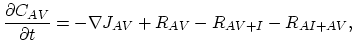 |
(3.50) |
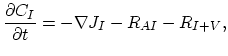 |
(3.51) |
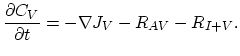 |
(3.52) |
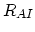 and
and 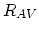 dopant/point defect pairing reactions rates defined as,
dopant/point defect pairing reactions rates defined as,
![$\displaystyle R_{AI} = \Bigl[ \sum_i k_{AI}^i K_{I}^i\Bigl(\frac{n_i}{n} \Bigr)^i \Bigr] \Bigl[ C_{A^+}C_{I^0}-\frac{C_{(AI)^+}}{K_{A+I}^0}\Bigr],$](img366.png) |
(3.53) |
![$\displaystyle R_{AV} = \Bigl[ \sum_i k_{AV}^i K_{V}^i\Bigl(\frac{n_i}{n} \Bigr)^i \Bigr] \Bigl[ C_{A^+}C_{V^0}-\frac{C_{(AV)^+}}{K_{A+V}^0}\Bigr].$](img367.png) |
(3.54) |
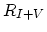 is Frankel recombination rate defined as,
is Frankel recombination rate defined as,
![$\displaystyle R_{I+V}= \Bigl[ \sum_{i,j} k_{I+V}^{i,j} K_{I}^i K_{V}^j\Bigl(\frac{n_i}{n} \Bigr)^{i+j} \Bigr][C_{I^0}C_{V^0}-C_{I^0}^{eq}C_{V^0}^{eq}].$](img369.png) |
(3.55) |
Finally, 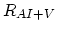 ,
, 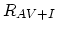 , and
, and 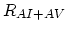 are net rates of the pair/defect and pair/pair reactions.
are net rates of the pair/defect and pair/pair reactions.
![$\displaystyle R_{AI+V}=\Bigl[ \sum_{i,j} k_{AI+V}^{i,j} K_{AI}^i K_{V}^j\Bigl(\...
...igr)^{i+j} \Bigr][C_{(AI)^+}C_{V^0}-K_{A+I}^0 C_{I^0}^{eq}C_{V^0}^{eq}C_{A^+}],$](img373.png) |
(3.56) |
![$\displaystyle R_{AV+I}=\Bigl[ \sum_{i,j} k_{AV+I}^{i,j} K_{AV}^i K_{I}^j\Bigl(\...
...igr)^{i+j} \Bigr][C_{(AV)^+}C_{I^0}-K_{A+V}^0 C_{V^0}^{eq}C_{I^0}^{eq}C_{A^+}],$](img374.png) |
(3.57) |
![$\displaystyle K_{A+I}^{0} K_{A+V}^{0} C_{I^0}^{eq} C_{V^0}^{eq} (C_{A^+})^2].$](img376.png) |
(3.58) |
We also need terms for the fluxes 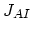 ,
, 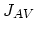 ,
, 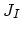 , and
, and 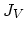 . Flux
. Flux 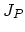 does not appear in the equations, because it is assumed that isolated dopant atoms are immobile and therefore
does not appear in the equations, because it is assumed that isolated dopant atoms are immobile and therefore 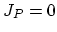 holds everywhere in the silicon bulk,
holds everywhere in the silicon bulk,
![$\displaystyle J_{AI}=-\Bigl[ \sum_{i} D_{(AI)^{i+1}} K_{AI}^i \Bigl(\frac{n_i}{...
...+C_{(AI)^{+}}\Bigl(\frac{n_i}{n} \Bigr)\nabla \Bigl(\frac{n}{n_i} \Bigr)\Bigr],$](img383.png) |
(3.59) |
![$\displaystyle J_{AV}=-\Bigl[ \sum_{i} D_{(AV)^{i+1}} K_{AV}^i \Bigl(\frac{n_i}{...
...+C_{(AV)^{+}}\Bigl(\frac{n_i}{n} \Bigr)\nabla \Bigl(\frac{n}{n_i} \Bigr)\Bigr],$](img384.png) |
(3.60) |
![$\displaystyle J_{I}=-\Bigl[ \sum_{i} D_{I^{i}} K_{I}^i \Bigl(\frac{n_i}{n} \Bigr) \Bigr] \nabla C_{I^{0}},$](img385.png) |
(3.61) |
![$\displaystyle J_{V}=-\Bigl[ \sum_{i} D_{V^{i}} K_{V}^i \Bigl(\frac{n_i}{n} \Bigr) \Bigr] \nabla C_{V^{0}}.$](img386.png) |
(3.62) |
In the equations (3.54)-(3.60) 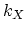 represents forward reaction rate coefficients, and
represents forward reaction rate coefficients, and  represents equilibrium constants.
represents equilibrium constants.
The model considered in this section correctly predicts the rapid diffusion in the peak region observed at high concentrations of phosphorus as well as the dependence of tail diffusion on the peak doping level, while remaining consistent with experimental results indicating that phosphorus diffusion is dominated by interstitials [30].



Next: 3.5 Boundary and Interface
Up: 3. Diffusion Phenomena in
Previous: 3.3 Equilibrium Diffusion
H. Ceric: Numerical Techniques in Modern TCAD
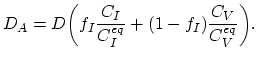
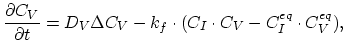
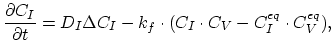
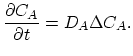
![]() ), the dopant-defect pairing reactions are fast enough to maintain the pair concentration near local equilibrium with the concentrations of isolated dopands and defects,
), the dopant-defect pairing reactions are fast enough to maintain the pair concentration near local equilibrium with the concentrations of isolated dopands and defects,
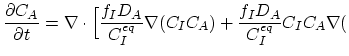 ln
ln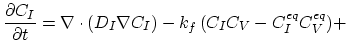
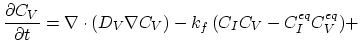
![]() , AI, AV, I, V, over all charge states for each species [30],
, AI, AV, I, V, over all charge states for each species [30],
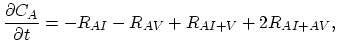
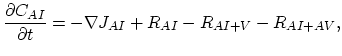
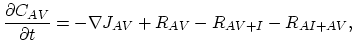
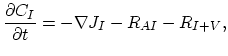
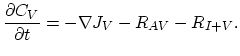
![$\displaystyle R_{AI} = \Bigl[ \sum_i k_{AI}^i K_{I}^i\Bigl(\frac{n_i}{n} \Bigr)^i \Bigr] \Bigl[ C_{A^+}C_{I^0}-\frac{C_{(AI)^+}}{K_{A+I}^0}\Bigr],$](img366.png)
![$\displaystyle R_{I+V}= \Bigl[ \sum_{i,j} k_{I+V}^{i,j} K_{I}^i K_{V}^j\Bigl(\frac{n_i}{n} \Bigr)^{i+j} \Bigr][C_{I^0}C_{V^0}-C_{I^0}^{eq}C_{V^0}^{eq}].$](img369.png)
![$\displaystyle R_{AI+V}=\Bigl[ \sum_{i,j} k_{AI+V}^{i,j} K_{AI}^i K_{V}^j\Bigl(\...
...igr)^{i+j} \Bigr][C_{(AI)^+}C_{V^0}-K_{A+I}^0 C_{I^0}^{eq}C_{V^0}^{eq}C_{A^+}],$](img373.png)
![$\displaystyle R_{AV+I}=\Bigl[ \sum_{i,j} k_{AV+I}^{i,j} K_{AV}^i K_{I}^j\Bigl(\...
...igr)^{i+j} \Bigr][C_{(AV)^+}C_{I^0}-K_{A+V}^0 C_{V^0}^{eq}C_{I^0}^{eq}C_{A^+}],$](img374.png)
![$\displaystyle R_{AI+AV}=\Bigl[ \sum_{i,j} k_{AI+AV}^{i,j} K_{AI}^i K_{AV}^j\Bigl(\frac{n_i}{n}\Bigr)^{i+j} \Bigr] [C_{(AI)^{+}}C_{(AV)^{+}}-$](img375.png)
![$\displaystyle J_{AI}=-\Bigl[ \sum_{i} D_{(AI)^{i+1}} K_{AI}^i \Bigl(\frac{n_i}{...
...+C_{(AI)^{+}}\Bigl(\frac{n_i}{n} \Bigr)\nabla \Bigl(\frac{n}{n_i} \Bigr)\Bigr],$](img383.png)
![$\displaystyle J_{I}=-\Bigl[ \sum_{i} D_{I^{i}} K_{I}^i \Bigl(\frac{n_i}{n} \Bigr) \Bigr] \nabla C_{I^{0}},$](img385.png)
![$\displaystyle J_{V}=-\Bigl[ \sum_{i} D_{V^{i}} K_{V}^i \Bigl(\frac{n_i}{n} \Bigr) \Bigr] \nabla C_{V^{0}}.$](img386.png)