



Next: 9 Dosis Conservation
Up: 8 Numerical Handling of
Previous: 4 Analytical Solution of
5 Numerical Handling of the Segregation Model
Let us assume that the segments 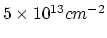 and
and 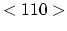 are comprised of
three-dimensional areas
are comprised of
three-dimensional areas 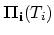 and
and 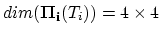 and
the connecting interface
and
the connecting interface 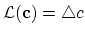 with two-dimensional area
with two-dimensional area
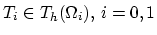 , respectively. The tetrahedralization of areas
, respectively. The tetrahedralization of areas 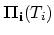 ,
,
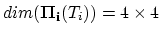 and the
triangulation of area
and the
triangulation of area 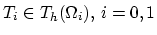 are denoted as
are denoted as
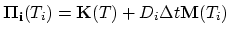 ,
,
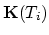 and
and
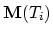 . We discretize (3.30) on the
element
. We discretize (3.30) on the
element
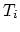 using a
linear basis function
using a
linear basis function 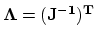 . After introducing the weak formulation of the equation and subsequently applying Green's theorem we have
. After introducing the weak formulation of the equation and subsequently applying Green's theorem we have
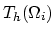 |
(194) |
where  is the boundary of the element
is the boundary of the element 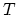 .
Assuming that
.
Assuming that
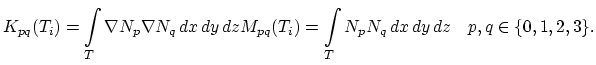 and
marking all inside faces of
and
marking all inside faces of  as
as
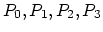 we have
we have
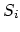 and we can write
and we can write
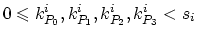 |
(195) |
In the standard finite element assembling procedure [5], we take into
account only the terms
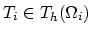 when
building up the stiffness matrix. Thereby the terms
when
building up the stiffness matrix. Thereby the terms
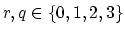 do not need to be considered because of their annihilation on the inside faces.
do not need to be considered because of their annihilation on the inside faces.
The term
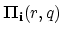 makes sense only on the interface area
makes sense only on the interface area 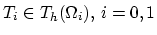 and
there it can be used to introduce the influence of
the species flux from the neighboring segment area
and
there it can be used to introduce the influence of
the species flux from the neighboring segment area 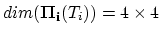 by applying
the segregation flux formula (3.65)
by applying
the segregation flux formula (3.65)
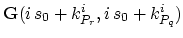 |
(196) |
After a usual assembling procedure on the tetrahedralization
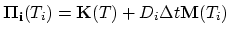 and
and
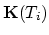 has been carried out and the global
stiffness matrix for both segment areas of the segregation problem has been built,
the interface inputs (3.133) for the segregation fluxes
has been carried out and the global
stiffness matrix for both segment areas of the segregation problem has been built,
the interface inputs (3.133) for the segregation fluxes 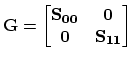 and
and 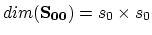 are evaluated on the triangulation
are evaluated on the triangulation
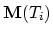 and
assembled into the global stiffness matrix according to the particular
assembling algorithm developed in this work.
and
assembled into the global stiffness matrix according to the particular
assembling algorithm developed in this work.
The numerical algorithm based on the concept described above is carried out in two steps.
Step 1.
We assemble the general matrix
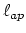 of the
problem for both segments, i.e., for both diffusion processes. The number
of points in segments
of the
problem for both segments, i.e., for both diffusion processes. The number
of points in segments 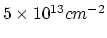 and
and 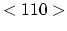 is denoted as
is denoted as 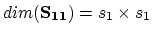 and
and 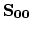 ,
respectively. The
general matrix has dimensions
,
respectively. The
general matrix has dimensions
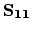 and the
inputs are correspondingly indexed.
The matrix is assembled by distributing
the inputs from matrix
and the
inputs are correspondingly indexed.
The matrix is assembled by distributing
the inputs from matrix
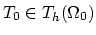 ,
,
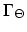 , defined for each
, defined for each
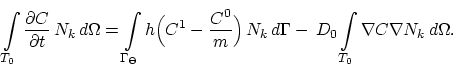
 |
(197) |
The 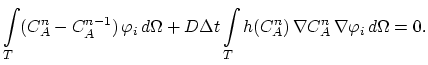 is the time step
of the discretisized time and
is the time step
of the discretisized time and
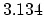 and
and
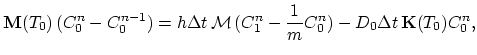 are stiffness and mass matrix defined on single
tetrahedra
are stiffness and mass matrix defined on single
tetrahedra 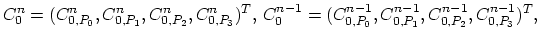 from
from
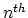
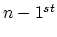 |
|
|
|
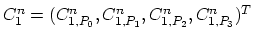 |
|
|
(198) |
Let us denote vertices of the element
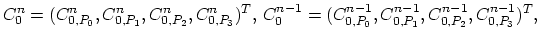 from the tetrahedralization
from the tetrahedralization
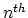 by
by
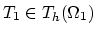 and their indexes in the segment
and their indexes in the segment 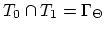 by
by
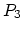 . Assembling means, for each
. Assembling means, for each
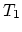 ,
and
,
and
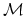 adding the term
adding the term
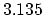 to
to
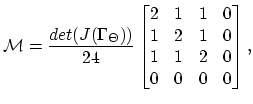 .
.
After this assembling procedure is carried out the general matrix
 has the following structure,
has the following structure,
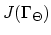 |
(199) |
Where
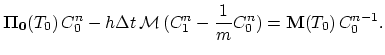 and
and
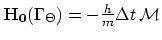 . The matrix
. The matrix
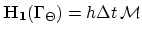 and
and
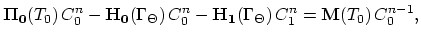 are the finite element discretizations of equation (3.30)
for the segments
are the finite element discretizations of equation (3.30)
for the segments 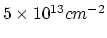 and
and 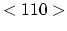 , respectively.
, respectively.
Step 2.
For the element
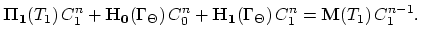 with one of it's faces
(
with one of it's faces
(
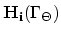 ) laying on the interface
) laying on the interface 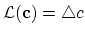 according to the idea presented above, weak formulation is,
according to the idea presented above, weak formulation is,
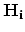 |
(200) |
The segregation term on the right side of (
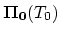 ) is
evaluated on the two-dimensional element
) is
evaluated on the two-dimensional element
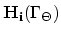 .
If we discretisize equation (
.
If we discretisize equation (
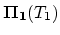 ) and take a backward Euler time scheme with time step
) and take a backward Euler time scheme with time step 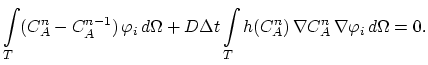 , we obtain for segment
, we obtain for segment 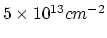 ,
,
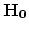 |
(201) |
where
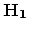 |
(202) |
are the values of the species concentration for the 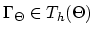 and
and 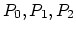 time step at the vertices of element
time step at the vertices of element 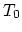 and analogously
and analogously
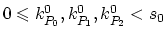 for
for
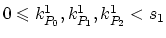 ,
,
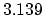 .
Without loosing generality we assume that verticex
.
Without loosing generality we assume that verticex 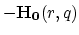 of the tetrahedras
of the tetrahedras 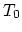 and
and 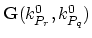 is the point which
doesn't belong to the interface
is the point which
doesn't belong to the interface 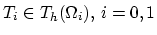 .
In that case the matrix
.
In that case the matrix
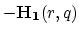 from (
from (
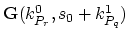 ) has a simple structure,
) has a simple structure,
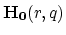 |
(203) |
where
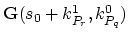 is the Jacobi matrix evaluated on element
is the Jacobi matrix evaluated on element
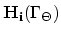 .
Using (3.134) we have,
.
Using (3.134) we have,
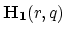 |
(204) |
We introduce now
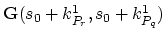 and
and
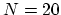 and write for the element
and write for the element 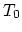 ,
,
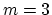 |
(205) |
and analogously for the element 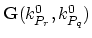 ,
,
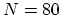 |
(206) |
In the following, for the sake of simplicity, we omit
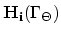 from
from
 and write
and write
 .
.
The contributions of
 and
and
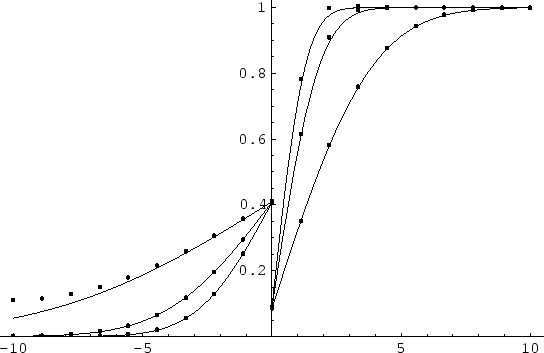 are already included in the
general matrix
are already included in the
general matrix
 by the assembling procedure
made in the first step, the build up of
by the assembling procedure
made in the first step, the build up of
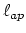 can now be completed by adding the inputs from matrix
can now be completed by adding the inputs from matrix
 and
and
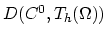 in order to take into account the segregation effect on interface
in order to take into account the segregation effect on interface
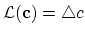 .
.
We denote the vertices of the element
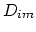 as
as
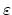 . In the tetrahedralization
. In the tetrahedralization
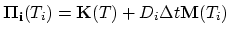 these points have indices
these points have indices
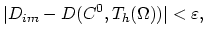 and indices
and indices
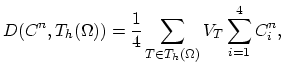 in the tetrahedralization
in the tetrahedralization
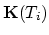 .
The actual implementation of the scheme (
.
The actual implementation of the scheme (
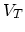 ) is for each
element
) is for each
element
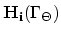 of the interface triangulation
of the interface triangulation
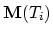 and for
and for
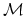 :
:
- adding the term
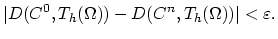 to the
input
to the
input
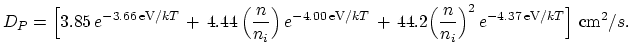
- adding the term
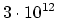 to the
to the
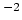
- adding the term
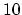 to
to

- adding the term
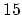 to the
to the
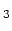 .
.
Now the assembling of the general matrix
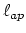 is
completed. These procedure is carried out for each time step of the simulation.
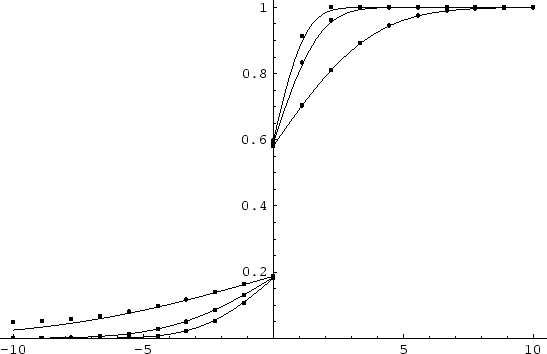
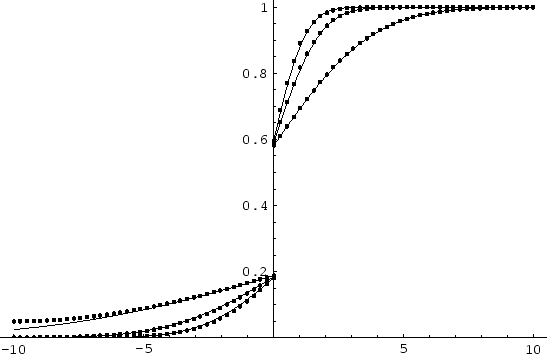
The numerical solution of the segregation problem is compared with an analytical solution on Figure 3.2.
is
completed. These procedure is carried out for each time step of the simulation.
The numerical solution of the segregation problem is compared with an analytical solution on Figure 3.2.
Figure:
The comparison between numerical (points) and analytical
solution (full line) for three different time steps in each figure
above. Two different spatial discretizations (N=20 and N=80 points) are used. Because of
the assumption of the infinite media by the derivation of analytical
solution there is a deviation of this solution from the numerical
one in the proximity of the point 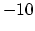 on the abscissa. Numerical solution considers finite segment with zero Neumann boundary condition at the
on the abscissa. Numerical solution considers finite segment with zero Neumann boundary condition at the 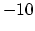 point.
point.
 , , 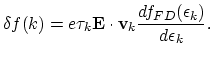
|
 , , 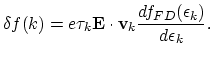
|
|




Next: 9 Dosis Conservation
Up: 8 Numerical Handling of
Previous: 4 Analytical Solution of
J. Cervenka: Three-Dimensional Mesh Generation for Device and Process Simulation
![]() and
and ![]() are comprised of
three-dimensional areas
are comprised of
three-dimensional areas ![]() and
and ![]() and
the connecting interface
and
the connecting interface ![]() with two-dimensional area
with two-dimensional area
![]() , respectively. The tetrahedralization of areas
, respectively. The tetrahedralization of areas ![]() ,
,
![]() and the
triangulation of area
and the
triangulation of area ![]() are denoted as
are denoted as
![]() ,
,
![]() and
and
![]() . We discretize (3.30) on the
element
. We discretize (3.30) on the
element
![]() using a
linear basis function
using a
linear basis function ![]() . After introducing the weak formulation of the equation and subsequently applying Green's theorem we have
. After introducing the weak formulation of the equation and subsequently applying Green's theorem we have
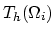
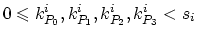
![]() of the
problem for both segments, i.e., for both diffusion processes. The number
of points in segments
of the
problem for both segments, i.e., for both diffusion processes. The number
of points in segments ![]() and
and ![]() is denoted as
is denoted as ![]() and
and ![]() ,
respectively. The
general matrix has dimensions
,
respectively. The
general matrix has dimensions
![]() and the
inputs are correspondingly indexed.
The matrix is assembled by distributing
the inputs from matrix
and the
inputs are correspondingly indexed.
The matrix is assembled by distributing
the inputs from matrix
![]() ,
,
![]() , defined for each
, defined for each
![]()
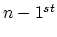
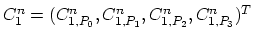
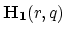
![]() and
and
![]() are already included in the
general matrix
are already included in the
general matrix
![]() by the assembling procedure
made in the first step, the build up of
by the assembling procedure
made in the first step, the build up of
![]() can now be completed by adding the inputs from matrix
can now be completed by adding the inputs from matrix
![]() and
and
![]() in order to take into account the segregation effect on interface
in order to take into account the segregation effect on interface
![]() .
.
![]() as
as
![]() . In the tetrahedralization
. In the tetrahedralization
![]() these points have indices
these points have indices
![]() and indices
and indices
![]() in the tetrahedralization
in the tetrahedralization
![]() .
The actual implementation of the scheme (
.
The actual implementation of the scheme (
![]() ) is for each
element
) is for each
element
![]() of the interface triangulation
of the interface triangulation
![]() and for
and for
![]() :
: