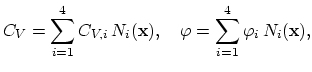Next: 3 The Sink/Source Term
Up: 4 Prediction of the
Previous: 1 Korhonen's Model
Korhonen's equation can be analytically solved for different cases of initial and boundary
conditions [51,7,80,83], however from the practical point of view, the most important solution is for the situation where the vacancy flux is blocked at the both ends of a finite line, i.e.
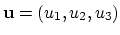 |
(232) |
on the segment ![$ [-l,0]$](img790.png) , assuming the initial vacancy concentration to be
, assuming the initial vacancy concentration to be
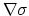 .
In this case, the solution of (4.21) is given in [83] as,
.
In this case, the solution of (4.21) is given in [83] as,
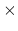 exp exp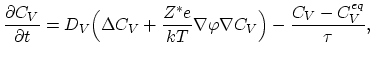 |
(233) |
where,
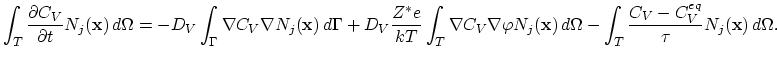 |
(234) |
is the steady-state solution and,
![$\displaystyle A_n=\frac{16n\pi[1-(-1)^n\text{exp}(\alpha/2)]}{(\alpha^2+4n^2\pi^2)^2}\Bigl(\text{sin}(n\pi\xi)+\frac{2n\pi}{\alpha}\text{cos}(n\pi\xi)\Bigr),$](img795.png) |
(235) |
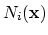 |
(236) |
For the sake of simplicity, in the equations (4.23)-(4.26) we used the substitutions,
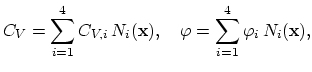 |
(237) |
For 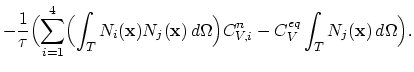 in Figure 4.2 and Figure 4.3 the distribution of the normalized vacancy concentration
in Figure 4.2 and Figure 4.3 the distribution of the normalized vacancy concentration 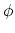 and the reduced hydrostatic pressure,
and the reduced hydrostatic pressure,
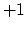 |
(238) |
are presented for different electromigration stressing times.
The stress build-up continues until the electromigration driving force is counter-balanced by intrinsic stress in the line.
That is the case in Figure 4.3 for 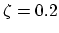 where the stress profile is a straight line.
The condition for the stress-electromigration equilibrium is,
where the stress profile is a straight line.
The condition for the stress-electromigration equilibrium is,
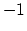 |
(239) |
Equation (4.29) is discussed in more detail in [48].
If for the given operating conditions the stress-electromigration equilibrium is reached before a critical stress threshold is build, no damage is produced and the interconnect is virtually ``immortal'' [48,49,47].




Next: 3 The Sink/Source Term
Up: 4 Prediction of the
Previous: 1 Korhonen's Model
J. Cervenka: Three-Dimensional Mesh Generation for Device and Process Simulation