


Next: 2.6 Grid Refinement
Up: 2. Grid Types
Previous: 2.4 Demands for the
Subsections
2.5 Demands for Finite Elements
Within Finite Elements the coefficients of the matrix
 shown in (2.8) and (2.9) can be generally expressed as [46][54][75]
shown in (2.8) and (2.9) can be generally expressed as [46][54][75]
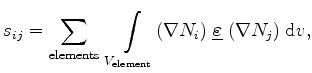 |
(2.19) |
respectively
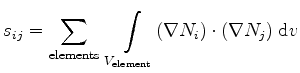 |
(2.20) |
for the element volumes
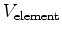 . The symbols
. The symbols 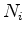 and
and 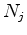 denote the Ansatzfunctions of the points
denote the Ansatzfunctions of the points  and
and 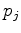 .
If
.
If
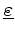 is a constant scalar within the tetrahedrons,
this in-product has a simple geometrical meaning and the compliance
(2.10)
is a constant scalar within the tetrahedrons,
this in-product has a simple geometrical meaning and the compliance
(2.10)
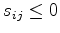 |
(2.21) |
leads to an angle criterion for each edge of the mesh [75]
Sum of dihedral angles:
Let
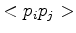 be an edge with be an edge with 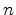 adjacent tetrahedra adjacent tetrahedra 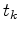 . For each tetrahedron . For each tetrahedron 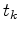 two planes exist which do not contain two planes exist which do not contain
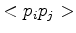 and which span a dihedral angle and which span a dihedral angle
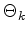 . The two planes share an edge with length . The two planes share an edge with length 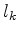 . The sum over . The sum over
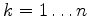 of the cotangent of of the cotangent of
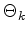 weighted by weighted by 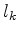 must be greater or equal than zero. must be greater or equal than zero.
|
Figure 2.10:
Three-dimensional grid criterion for Finite Elements.
|
![\includegraphics[width=7.0cm]{picsconveps/dihedra1.eps}](img179.png)
Dihedral angle 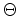 of the edge
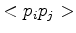 of a tetrahedron
|
![\includegraphics[width=7.0cm]{picsconveps/dihedra2.eps}](img180.png)
Dihedral angles around the edge
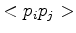 , arisen from the four tetrahedrons which share the edge
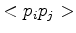
|
|
Within Figure 2.10 the criterion is clarified. In Figure 2.10(a) the dihedral angle of the edge
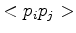 is shown. It is the angle between the faces which do not contain the edge
is shown. It is the angle between the faces which do not contain the edge
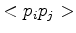 . Here,
. Here, 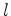 is the length of the edge opposing to
is the length of the edge opposing to
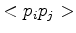 .
In Figure 2.10(b) all the tetrahedrons connected to
.
In Figure 2.10(b) all the tetrahedrons connected to
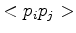 are shown. Each of the participating tetrahedrons
are shown. Each of the participating tetrahedrons 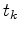 spans its own dihedral angle
spans its own dihedral angle 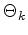 to
to
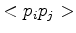 .
.
In two dimensions the criterion (2.22) is also valid. The two triangles connected to
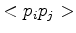 can be considered as tetrahedrons with the same (small) edge
can be considered as tetrahedrons with the same (small) edge 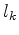 , which can be canceled out of the summation, and the dihedral angle of the edge
, which can be canceled out of the summation, and the dihedral angle of the edge
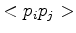 simplifies to the angle between the two edges of the triangle which do not contain this edge.
simplifies to the angle between the two edges of the triangle which do not contain this edge.
Figure 2.11:
Two-dimensional mesh criterion for Finite Elements
|
|
The dihedral angle reduces to
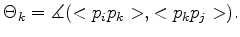 |
(2.23) |
As shown in Figure 2.11 in two dimensions exactly two triangles are connected by each edge and (2.22) simplifies to
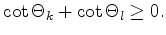 |
(2.24) |
With the following transformation and knowing that
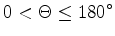 or or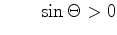 |
(2.25) |
we get
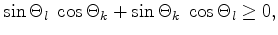 |
(2.26) |
which is equivalent to
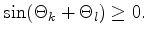 |
(2.27) |
Therefore,
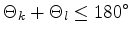 |
(2.28) |
is the well-known formulation for two dimensions. This is the same criterion as for Box Integration, given in (2.17).
Therefore, the general two-dimensional grid criterion for Finite Boxes and Finite Elements results in the same formulation which is satisfied if the tessellation of the grid points is a Delaunay tessellation. In three dimensions, the criterion for Finite Boxes and Finite Elements differ. Detailed information of the three-dimensional differences can be found in [13][14][19][28].



Next: 2.6 Grid Refinement
Up: 2. Grid Types
Previous: 2.4 Demands for the
J. Cervenka: Three-Dimensional Mesh Generation for Device and Process Simulation
![]() shown in (2.8) and (2.9) can be generally expressed as [46][54][75]
shown in (2.8) and (2.9) can be generally expressed as [46][54][75]
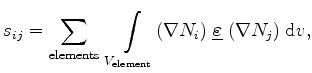
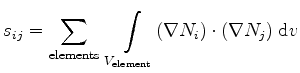
![]() is shown. It is the angle between the faces which do not contain the edge
is shown. It is the angle between the faces which do not contain the edge
![]() . Here,
. Here, ![]() is the length of the edge opposing to
is the length of the edge opposing to
![]() .
In Figure 2.10(b) all the tetrahedrons connected to
.
In Figure 2.10(b) all the tetrahedrons connected to
![]() are shown. Each of the participating tetrahedrons
are shown. Each of the participating tetrahedrons ![]() spans its own dihedral angle
spans its own dihedral angle ![]() to
to
![]() .
.
![]() can be considered as tetrahedrons with the same (small) edge
can be considered as tetrahedrons with the same (small) edge ![]() , which can be canceled out of the summation, and the dihedral angle of the edge
, which can be canceled out of the summation, and the dihedral angle of the edge
![]() simplifies to the angle between the two edges of the triangle which do not contain this edge.
simplifies to the angle between the two edges of the triangle which do not contain this edge.