


Next: 2.5 Demands for Finite
Up: 2. Grid Types
Previous: 2.3 Grid Requirements
Subsections
2.4 Demands for the Box Integration Method
In association with the Box Integration discretization (refer Chapter 3, equations (3.32) and (3.57)), equation (2.10) can be rewritten as
where 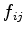 denotes a positive material parameter (the permittivity for the Laplace equation,
denotes a positive material parameter (the permittivity for the Laplace equation,  for the diffusion equation). The parameters
for the diffusion equation). The parameters 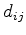 and
and 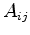 are geometrical values which are determined by the geometry of the grid elements only.
are geometrical values which are determined by the geometry of the grid elements only.
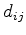 is the length of the edge
is the length of the edge
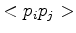 between the points
between the points  and
and 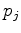 (positive), and
(positive), and 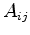 the coupling area between the two points.
As a geometrical consequence the coupling areas and point distances are symmetrical
the coupling area between the two points.
As a geometrical consequence the coupling areas and point distances are symmetrical
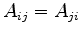 and and |
(2.12) |
and it is also of advantage and plausible to use a symmetrical material parameter
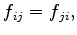 |
(2.13) |
which finally delivers a symmetrical system matrix
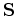 .
Consequentially, relation (2.11) is only satisfied if the coupling area is positive
.
Consequentially, relation (2.11) is only satisfied if the coupling area is positive
However, such positive coupling areas are guaranteed by a Delaunay tessellation of the point set. In general, the definition of a Delaunay triangulation is based on the Voronoi diagram by the principle of duality [42] and will be introduced in the following section.
Let
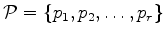 be a finite set of points in a sub-domain
be a finite set of points in a sub-domain 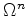 of the
of the 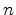 -dimensional space
-dimensional space
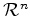 .
.
A Voronoi region 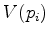 is the set of all points of
is the set of all points of 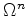 that are closer to
that are closer to  than to any other point of
than to any other point of
 .
.
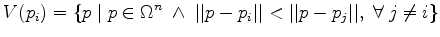 |
(2.15) |
The resulting Voronoi regions 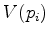 form a Voronoi tessellation of
form a Voronoi tessellation of 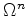 (without overlap or exclusion)
(without overlap or exclusion)
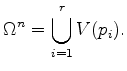 |
(2.16) |
By connecting the vertices  ,
, 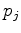 of two touching Voronoi regions
of two touching Voronoi regions 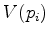 and
and 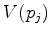 , a Delaunay edge
, a Delaunay edge
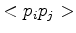 is constructed. The pool of all Delaunay edges builds the Delaunay mesh of the point set
is constructed. The pool of all Delaunay edges builds the Delaunay mesh of the point set
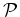 .
This Delaunay graph shows the following properties:
.
This Delaunay graph shows the following properties:
Two points  and
and 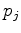 form a Delaunay edge
form a Delaunay edge
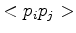 if and only if there exists an
if and only if there exists an 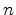 -dimensional sphere which passes
-dimensional sphere which passes  and
and 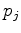 and contains no other points of
and contains no other points of
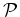 .
.
(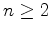 ) Three non-collinear points
) Three non-collinear points 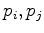 , and
, and 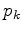 form a Delaunay triangle
form a Delaunay triangle
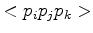 if and only if there exists an
if and only if there exists an 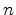 -dimensional sphere which passes
-dimensional sphere which passes 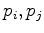 , and
, and 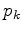 and contains no other points of
and contains no other points of
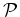 .
.
(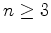 ) Four non-coplanar points
) Four non-coplanar points
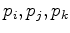 , and
, and 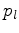 form a Delaunay tetrahedron
form a Delaunay tetrahedron
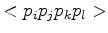 if and only if there exists an
if and only if there exists an 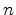 -dimensional sphere which passes
-dimensional sphere which passes
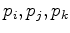 , and
, and 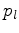 and contains no other points of
and contains no other points of
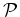 .
.
These formulations can be expressed in a mathematical way:
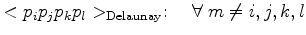
Here, 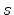 is the center of the
is the center of the 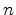 -dimensional sphere. Analogous formulations can be found for Delaunay triangles and lines. A Delaunay tetrahedron implies that it must consist of Delaunay triangles and Delaunay edges.
-dimensional sphere. Analogous formulations can be found for Delaunay triangles and lines. A Delaunay tetrahedron implies that it must consist of Delaunay triangles and Delaunay edges.
Figure 2.3:
A two-dimensional Voronoi box of the point 
|
|
A two-dimensional Voronoi box is shown in Figure 2.3.
In two dimensions the coupling area 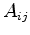 degenerates to the length of the Voronoi edge, which bisects the edge
degenerates to the length of the Voronoi edge, which bisects the edge
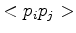 and connects the two center-points of the outer-circles of the triangles
and connects the two center-points of the outer-circles of the triangles
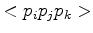 and
and
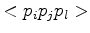 .
.
By splitting this area 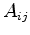 into the parts
into the parts  and
and 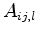 arising from the involved triangles
arising from the involved triangles
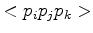 and
and
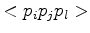 , respectively, the situation depicted in Figure 2.4(a) is obtained.
In this context, for each triangle
, respectively, the situation depicted in Figure 2.4(a) is obtained.
In this context, for each triangle
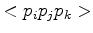 the possibilities shown in Figure 2.4(c) and Figure 2.4(d) exist.
The portion
the possibilities shown in Figure 2.4(c) and Figure 2.4(d) exist.
The portion  can lie inside or outside the half plane which is spanned by the straight line, built by
can lie inside or outside the half plane which is spanned by the straight line, built by  and
and 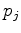 , and the point
, and the point 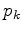 . By definition an inside-portion
. By definition an inside-portion  is signed positive (Figure 2.4(c)) and signed negative if it lies outside (Figure 2.4(d)).
In consideration of non-overlapping Voronoi boxes, the sum of both portions has to be positive.
And with geometrical considerations (refer Figure 2.4(b))
is signed positive (Figure 2.4(c)) and signed negative if it lies outside (Figure 2.4(d)).
In consideration of non-overlapping Voronoi boxes, the sum of both portions has to be positive.
And with geometrical considerations (refer Figure 2.4(b))
or equivalently,
has to be satisfied.
Figure 2.4:
A detail of the Voronoi Region shown before.
|
![\includegraphics[width=7.5cm]{picsconveps/splitvoro.eps}](img137.png)
The components of the Voronoi regions of the triangles
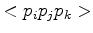 and
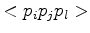 .
|
![\includegraphics[width=6.8cm]{picsconveps/exvoro.eps}](img139.png)
The angle criterion for two dimensions. The marginal case with 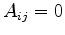 is reached if 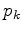 lies at the outer-circle of
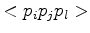 .
|
![\includegraphics[width=7.5cm]{picsconveps/oktri.eps}](img142.png)
The center 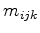 of the outer-circle of the triangle
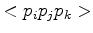 lies in the half plane
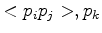 . The portion of the coupling area is positive
 .
|
![\includegraphics[width=6.8cm]{picsconveps/badtri.eps}](img144.png)
The center 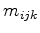 of the outer-circle of the triangle
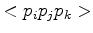 lies outside of the half plane
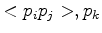 . The portion of the coupling area is negative
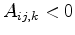 .
|
|
Figure 2.5:
Valid and invalid tessellations of two triangles.
|
![$\textstyle \parbox{0.45\linewidth}{
\includegraphics[scale=0.45]{picsconveps/v1}}$](img145.png)
Valid tessellation of two triangles,
 and
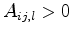
|
![$\textstyle \parbox{0.45\linewidth}{
\includegraphics[scale=0.45]{picsconveps/v15}}$](img147.png)
Valid tessellation of the two triangles,
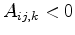 ,
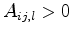 and in sum 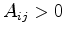 , a non-overlapping Voronoi box remains
|
![$\textstyle \parbox{0.45\linewidth}{
\includegraphics[scale=0.45]{picsconveps/v25}}$](img149.png)
Invalid tessellation of the two triangles,
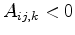 ,
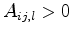 , but
 , an overlapping Voronoi box remains
|
![$\textstyle \parbox{0.45\linewidth}{
\includegraphics[scale=0.45]{picsconveps/v3}}$](img151.png)
Invalid tessellation of the two triangles,
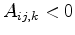 and
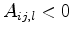 , also an overlapping Voronoi box is built
|
|
Consequently it follows that if the point 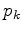 lies inside the outer-circle of the triangle
lies inside the outer-circle of the triangle
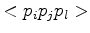 , relation (2.18) is violated. If
, relation (2.18) is violated. If 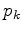 lies outside or directly on the circle (marginal case), the relation is satisfied. This criterion must be fulfilled for each neighboring triangle-pair of the mesh. Examples for valid and invalid (overlapping) two-dimensional Voronoi edges are shown in Figure 2.5.
lies outside or directly on the circle (marginal case), the relation is satisfied. This criterion must be fulfilled for each neighboring triangle-pair of the mesh. Examples for valid and invalid (overlapping) two-dimensional Voronoi edges are shown in Figure 2.5.
With other words:
There must not be any grid point, which lies inside the outer-circle of each triangle.
This is known as the Delaunay criterion for two dimensions.
While the above criterion can be satisfied for each point set, for given geometry and boundary constrains the criterion must be formulated more strictly.
In that case, (2.14) must also be satisfied on the boundaries. The coupling area 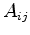 between two boundary points
between two boundary points  and
and 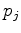 must not be negative (see Figure 2.6). This means, all centers of the outer-circles of the boundary triangles must lie within the boundaries. This type of triangulation is called a Constrained Delaunay Triangulation and the criterion can be formulated as:
must not be negative (see Figure 2.6). This means, all centers of the outer-circles of the boundary triangles must lie within the boundaries. This type of triangulation is called a Constrained Delaunay Triangulation and the criterion can be formulated as:
There must not be any grid point, which lies inside the half circles constructed by the boundary lines.
Figure 2.6:
Valid and invalid Voronoi edges at the surface. At the marginal case, the center of the outer-circle lies at the surface.
|
![\includegraphics[width=7.0cm]{picsconveps/vorob1}](img153.png)
Valid triangulation at the boundary, 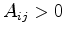
|
![\includegraphics[width=7.5cm]{picsconveps/vorob2}](img155.png)
Invalid triangulation of the boundary, 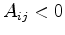
|
|
2.4.3 Three-Dimensional Criterion
Figure 2.7:
The coupling areas of a three-dimensional tetrahedral Delaunay grid around the point  .
.
|
![\includegraphics[width=6.9cm]{htmlpicsconveps/newbox}](img156.png)
Typical Voronoi box around a grid point 
|
![\includegraphics[width=6.9cm]{htmlpicsconveps/box2}](img157.png)
Detail of the box, the coupling area between the point  and 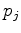
|
![\includegraphics[width=6.9cm]{htmlpicsconveps/box3}](img158.png)
Viewing the coupling area along the edge
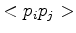
|
![\includegraphics[width=6.9cm]{htmlpicsconveps/box5}](img159.png)
Separated situation
|
|
For the three-dimensional case such an area 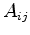 is shown in Figure 2.7(b), which is based on a typical Voronoi box as shown in Figure 2.7(a). This area can be split into the different components due to each tetrahedron (shown in Figure 2.7(c) and the separated situation in Figure 2.7(d)).
The different parts are spanning triangles. Each triangle is defined by the center of the examined edge, the center of the outer-circle of the appropriate triangle and the center of the outer-sphere of the tetrahedron.
is shown in Figure 2.7(b), which is based on a typical Voronoi box as shown in Figure 2.7(a). This area can be split into the different components due to each tetrahedron (shown in Figure 2.7(c) and the separated situation in Figure 2.7(d)).
The different parts are spanning triangles. Each triangle is defined by the center of the examined edge, the center of the outer-circle of the appropriate triangle and the center of the outer-sphere of the tetrahedron.
Analogous to two dimensions, the sign of such an area of a box part that lies inside the tetrahedrons must be positive, outside areas have a negative sign, and generally, the areas are not allowed to overlap.
Figure 2.8:
The coupling areas between two points of different tetrahedrons.
|
![$\textstyle \parbox{6.7cm}{\center
\includegraphics[height=7.5cm]%width=6.5cm]
{picsconveps/detail11}
}$](img160.png)
Valid coupling area, the portions of both tetrahedrons are positive
|
![$\textstyle \parbox{6.7cm}{\center
\includegraphics[height=7.5cm]%width=6.5cm]
{picsconveps/detail22}
}$](img161.png)
Valid coupling area, one positive and one negative portion, in sum a positive, non-overlapping area remains
|
![$\textstyle \parbox{6.7cm}{\center
\includegraphics[height=7.5cm]%width=6.5cm]
{picsconveps/detail44}
}$](img162.png)
Invalid coupling, one positive and one negative coupling portion, an overlapping area is constructed
|
![$\textstyle \parbox{6.7cm}{\center
\includegraphics[height=8cm]%width=6.5cm]
{picsconveps/detail55}
}$](img163.png)
Invalid coupling, both portions are negative, a negative and overlapping area remains
|
|
Such details of valid boxes are shown in Figure 2.8(a) and 2.8(b).
In the first example, both area parts are positive. In the second example, one area is negative, but smaller than the other one, which also leads to a valid grid.
Invalid details with a resulting negative sum of the areas are shown in Figure 2.8(c) and 2.8(d).
Such a tessellation of a point set is also a Delaunay tessellation and the criterion reads as follows:
There must not be any grid point, which lies inside the outer-sphere of each tetrahedron.
|
But different to the two-dimensional case, no simplified angle criterion can be declared for three dimensions.
Also for three-dimensional Delaunay grids, the coupling area 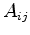 between two boundary points
between two boundary points  and
and 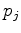 must not be negative. The three-dimensional behavior is shown in Figure 2.9 and the criterion can be formulated:
must not be negative. The three-dimensional behavior is shown in Figure 2.9 and the criterion can be formulated:
There must not be any grid point, which lies inside the half spheres constructed by the boundary triangles.
Figure 2.9:
Valid and invalid Voronoi faces at the surface. At the marginal case, the center of the outer-sphere lies at the surface.
|
![\includegraphics[width=7.2cm]{picsconveps/oktet3}](img164.png)
Valid surface triangulation, coupling areas at the surface are positive, the center of the outer-sphere of the tetrahedron lies inside
|
![\includegraphics[width=7.2cm]{picsconveps/badtet3}](img165.png)
Invalid surface triangulation, negative coupling areas, the center of the outer-sphere of the tetrahedron lies outside
|
|



Next: 2.5 Demands for Finite
Up: 2. Grid Types
Previous: 2.3 Grid Requirements
J. Cervenka: Three-Dimensional Mesh Generation for Device and Process Simulation
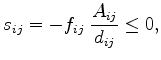
![]() be a finite set of points in a sub-domain
be a finite set of points in a sub-domain ![]() of the
of the ![]() -dimensional space
-dimensional space
![]() .
.
![]() is the set of all points of
is the set of all points of ![]() that are closer to
that are closer to ![]() than to any other point of
than to any other point of
![]() .
.
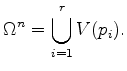
![]() and
and ![]() form a Delaunay edge
form a Delaunay edge
![]() if and only if there exists an
if and only if there exists an ![]() -dimensional sphere which passes
-dimensional sphere which passes ![]() and
and ![]() and contains no other points of
and contains no other points of
![]() .
.
![]() ) Three non-collinear points
) Three non-collinear points ![]() , and
, and ![]() form a Delaunay triangle
form a Delaunay triangle
![]() if and only if there exists an
if and only if there exists an ![]() -dimensional sphere which passes
-dimensional sphere which passes ![]() , and
, and ![]() and contains no other points of
and contains no other points of
![]() .
.
![]() ) Four non-coplanar points
) Four non-coplanar points
![]() , and
, and ![]() form a Delaunay tetrahedron
form a Delaunay tetrahedron
![]() if and only if there exists an
if and only if there exists an ![]() -dimensional sphere which passes
-dimensional sphere which passes
![]() , and
, and ![]() and contains no other points of
and contains no other points of
![]() .
.
![]()

![]() is the center of the
is the center of the ![]() -dimensional sphere. Analogous formulations can be found for Delaunay triangles and lines. A Delaunay tetrahedron implies that it must consist of Delaunay triangles and Delaunay edges.
-dimensional sphere. Analogous formulations can be found for Delaunay triangles and lines. A Delaunay tetrahedron implies that it must consist of Delaunay triangles and Delaunay edges.
![]() into the parts
into the parts ![]() and
and ![]() arising from the involved triangles
arising from the involved triangles
![]() and
and
![]() , respectively, the situation depicted in Figure 2.4(a) is obtained.
In this context, for each triangle
, respectively, the situation depicted in Figure 2.4(a) is obtained.
In this context, for each triangle
![]() the possibilities shown in Figure 2.4(c) and Figure 2.4(d) exist.
The portion
the possibilities shown in Figure 2.4(c) and Figure 2.4(d) exist.
The portion ![]() can lie inside or outside the half plane which is spanned by the straight line, built by
can lie inside or outside the half plane which is spanned by the straight line, built by ![]() and
and ![]() , and the point
, and the point ![]() . By definition an inside-portion
. By definition an inside-portion ![]() is signed positive (Figure 2.4(c)) and signed negative if it lies outside (Figure 2.4(d)).
In consideration of non-overlapping Voronoi boxes, the sum of both portions has to be positive.
And with geometrical considerations (refer Figure 2.4(b))
is signed positive (Figure 2.4(c)) and signed negative if it lies outside (Figure 2.4(d)).
In consideration of non-overlapping Voronoi boxes, the sum of both portions has to be positive.
And with geometrical considerations (refer Figure 2.4(b))
![]() lies inside the outer-circle of the triangle
lies inside the outer-circle of the triangle
![]() , relation (2.18) is violated. If
, relation (2.18) is violated. If ![]() lies outside or directly on the circle (marginal case), the relation is satisfied. This criterion must be fulfilled for each neighboring triangle-pair of the mesh. Examples for valid and invalid (overlapping) two-dimensional Voronoi edges are shown in Figure 2.5.
lies outside or directly on the circle (marginal case), the relation is satisfied. This criterion must be fulfilled for each neighboring triangle-pair of the mesh. Examples for valid and invalid (overlapping) two-dimensional Voronoi edges are shown in Figure 2.5.
![]() between two boundary points
between two boundary points ![]() and
and ![]() must not be negative (see Figure 2.6). This means, all centers of the outer-circles of the boundary triangles must lie within the boundaries. This type of triangulation is called a Constrained Delaunay Triangulation and the criterion can be formulated as:
must not be negative (see Figure 2.6). This means, all centers of the outer-circles of the boundary triangles must lie within the boundaries. This type of triangulation is called a Constrained Delaunay Triangulation and the criterion can be formulated as:
![]() is shown in Figure 2.7(b), which is based on a typical Voronoi box as shown in Figure 2.7(a). This area can be split into the different components due to each tetrahedron (shown in Figure 2.7(c) and the separated situation in Figure 2.7(d)).
The different parts are spanning triangles. Each triangle is defined by the center of the examined edge, the center of the outer-circle of the appropriate triangle and the center of the outer-sphere of the tetrahedron.
is shown in Figure 2.7(b), which is based on a typical Voronoi box as shown in Figure 2.7(a). This area can be split into the different components due to each tetrahedron (shown in Figure 2.7(c) and the separated situation in Figure 2.7(d)).
The different parts are spanning triangles. Each triangle is defined by the center of the examined edge, the center of the outer-circle of the appropriate triangle and the center of the outer-sphere of the tetrahedron.
![]() between two boundary points
between two boundary points ![]() and
and ![]() must not be negative. The three-dimensional behavior is shown in Figure 2.9 and the criterion can be formulated:
must not be negative. The three-dimensional behavior is shown in Figure 2.9 and the criterion can be formulated: