


Next: 3.2 The Diffusion Equation
Up: 3. The Box Integration
Previous: 3. The Box Integration
Subsections
3.1 The Poisson Equation
The Poisson equation is fundamental for all electrical applications. The derivation is shown for a stationary electric field [26]. For the derivation, the material parameters may be inhomogeneous, locally dependent but not a function of the electric field. In this section, the principle of the discretization is demonstrated.
In the case of a low field dependency, a recursive reinsertion of newly derived material parameters may result in stable solutions [54]. A highly nonlinear behavior has to be managed by linearization and Newton iterations, for instance [2][4][60].
The Maxwell equations for a stationary electric field reduce to
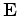 and
and
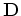 are related by the permittivity
are related by the permittivity
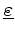
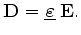 |
(3.3) |
Physical properties require that the permittivity tensor
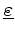 is symmetric and positive definite for lossless media (or a positive scalar for isotropic media).
Equation (3.1) is satisfied implicitly by introducing the electric potential
is symmetric and positive definite for lossless media (or a positive scalar for isotropic media).
Equation (3.1) is satisfied implicitly by introducing the electric potential 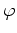
Combing (3.1)-(3.4), the Maxwell equations can be rewritten as
This can be transformed to its integral formulation. By applying the Gaussian integral formula (3.5) results in
Equation (3.6) must be fulfilled within any arbitrary volume 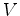 , with
, with
 being the surface of this volume.
While performing Box Integration, this formula must be satisfied in the
Voronoi boxes of each grid point. In Figure 3.1 a typical
Voronoi box of a point
being the surface of this volume.
While performing Box Integration, this formula must be satisfied in the
Voronoi boxes of each grid point. In Figure 3.1 a typical
Voronoi box of a point  , belonging to all the tetrahedrons connected to the point
, belonging to all the tetrahedrons connected to the point  , can be seen.
The integration can be split into the integration over the different box parts, caused by all the tetrahedrons
, can be seen.
The integration can be split into the integration over the different box parts, caused by all the tetrahedrons
 which share the same point
which share the same point 
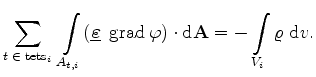 |
(3.7) |
Such a part of the Voronoi box within the tetrahedron
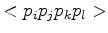 is shown in
Figure 3.2.
Each part around the point
is shown in
Figure 3.2.
Each part around the point  can also be split into the three area contributions that are caused by the different edges
can also be split into the three area contributions that are caused by the different edges
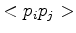 ,
,
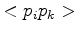 and
and
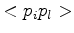 (see Figure 3.3)
(see Figure 3.3)
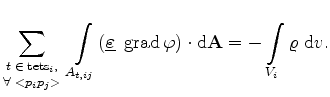 |
(3.8) |
Figure 3.1:
Tetrahedrons around point  with the resulting Voronoi box constructed by these tetrahedrons.
with the resulting Voronoi box constructed by these tetrahedrons.
|
|
Figure 3.2:
Box parts of the tetrahedron
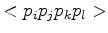 with drawn outer-sphere
with drawn outer-sphere 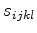 of the tetrahedron and outer-circle
of the tetrahedron and outer-circle 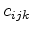 of the triangle
of the triangle
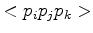 .
.
|
|
Figure 3.3:
Different Voronoi faces which share the point  of a tetrahedron.
of a tetrahedron.
|
|
Using Box Integration, an approximation of first order is usually assumed, which means that the electric potential 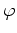 within one tetrahedron is a linear function along the axes or, in other words, the electric field
within one tetrahedron is a linear function along the axes or, in other words, the electric field
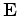 is constant within each tetrahedron. Material parameters are assumed to be constant within the tetrahedron, too. The electric charge density
is constant within each tetrahedron. Material parameters are assumed to be constant within the tetrahedron, too. The electric charge density  on the right-hand-side is assumed to be constant within the whole Voronoi box as well and can therefore be analytically calculated and written as the electric charge
on the right-hand-side is assumed to be constant within the whole Voronoi box as well and can therefore be analytically calculated and written as the electric charge 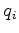 of the Voronoi box of the point
of the Voronoi box of the point  , which results in
, which results in
As in the usual applications the permittivity tensor reduces to a scalar, which means the electric displacement and the electric field have the same direction, it follows
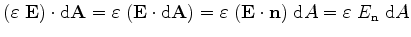 |
(3.10) |
and equation (3.9) can be simplified to
Usually the integral (3.11) is approximated by
with
Figure 3.4:
A detail of the tetrahedron
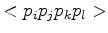 shown in Figure 3.3 which shows the coupling Voronoi region between the point
shown in Figure 3.3 which shows the coupling Voronoi region between the point  and
and 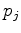 . This region can be split into the two triangular components
. This region can be split into the two triangular components  and
and 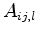 which are spawned by the midpoint
which are spawned by the midpoint 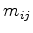 of the edge
of the edge
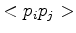 , the midpoint
, the midpoint 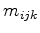 of the outer-circle of the triangle
of the outer-circle of the triangle
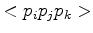 and the midpoint
and the midpoint 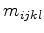 of the outer-sphere of the tetrahedron
of the outer-sphere of the tetrahedron
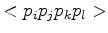 , or
, or 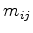 ,
, 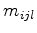 , and
, and 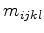 , respectively.
, respectively.
|
|
Figure 3.5:
Potential distribution between two grid points  and
and 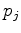 with different permittivities.
with different permittivities.
|
|
An estimation of the validity of this approximation based on the homogenous Poisson equation (Laplace equation) will be explained under the conditions shown in Figure 3.4.
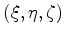 spans a local Cartesian coordinate system with origin
spans a local Cartesian coordinate system with origin  .
In the one-dimensional case and with constant permittivity the potential varies linearly with position as
.
In the one-dimensional case and with constant permittivity the potential varies linearly with position as
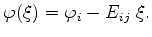 |
(3.14) |
Whereas with non-constant permittivity we have at first order
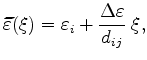 |
(3.15) |
with
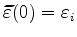 and and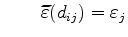 |
(3.16) |
and therefore,
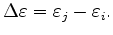 |
(3.17) |
The continuity of the electric displacement
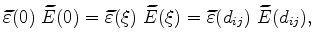 |
(3.18) |
with
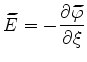 |
(3.19) |
delivers the deformed distribution of
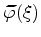
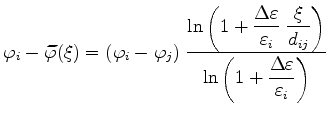 |
(3.20) |
and therefore,
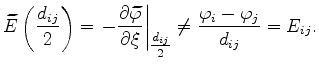 |
(3.21) |
The resulting potential distributions
 between
between  and
and 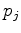 for different values of
for different values of
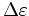 are shown in Figure 3.5. The overestimation of the electric field
are shown in Figure 3.5. The overestimation of the electric field
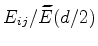 in the middle of the grid element in dependence of the permittivity change inside the element is shown in Figure 3.6.
According to this figure, a limit for the validity of approximation (3.13) can be defined by
in the middle of the grid element in dependence of the permittivity change inside the element is shown in Figure 3.6.
According to this figure, a limit for the validity of approximation (3.13) can be defined by
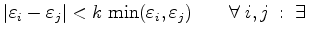 edge edge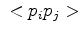 |
(3.22) |
or a limit for continuously defined permittivity
With
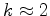 , the estimation error of
, the estimation error of 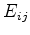 is limited to 10%.
is limited to 10%.
Figure 3.6:
Ratio of the approximated electric field 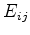 to the exact solution
to the exact solution
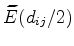 at the center of the control volume.
at the center of the control volume.
|
|
On a three-dimensional grid (refer to Figure 3.4), the spatial derivatives of
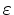 cause an additional contribution to the discretization error. With linear interpolation of
cause an additional contribution to the discretization error. With linear interpolation of
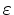 and
and 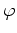 , equation (3.11) results in
, equation (3.11) results in
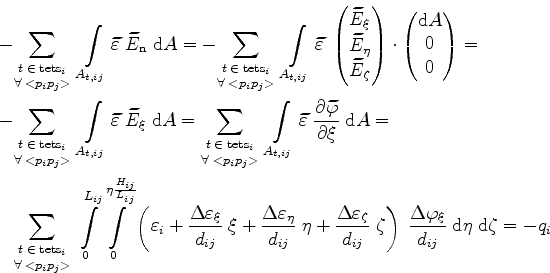 |
(3.24) |
and with

The first addend of equation (3.25) equals the value given by discretization (3.12) and (3.13) whereas the remaining terms cause an additional discretization error.
Often the derivative components of neighboring tetrahedrons compensate each other, but not always. Even the lengths of  and
and  are not limited to lie within the tetrahedron ranges (for instance, obtuse angled triangles for two dimensions) and a limitation for this approximation is difficult. For the whole simulation domain the estimation
are not limited to lie within the tetrahedron ranges (for instance, obtuse angled triangles for two dimensions) and a limitation for this approximation is difficult. For the whole simulation domain the estimation
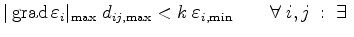 edge edge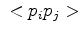 |
(3.26) |
seems plausible, but is too pessimistic as in most cases 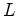 and
and 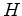 have the same order of magnitude as their based tetrahedrons. The previously derived estimation (3.23) is therefore also applicable to the three-dimensional case.
have the same order of magnitude as their based tetrahedrons. The previously derived estimation (3.23) is therefore also applicable to the three-dimensional case.
Another common approximation method for the effective permittivity
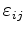 is [27]
is [27]
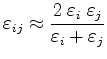 |
(3.27) |
which shows the behavior of a serial connection of two capacitors (or resistors for electrical flow fields). This approximation has the advantage that if the permittivity (more likely for the conductivity) is zero in a Voronoi box, no flux enters the box. Nevertheless, this zero flux leaves the electric potential of the included grid point undefined and may cause problems for the equation solver, applied later on.
However, equation (3.11) is discretized as
In compliance with the decomposition of the Voronoi regions in Section
2.4.3, 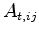 is the right signed value of the Voronoi area between
is the right signed value of the Voronoi area between  and
and 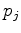 of the tetrahedron
of the tetrahedron 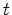 . Which means in detail, area portions with
. Which means in detail, area portions with
- outer-circle inside the appropriate triangle and outer-sphere inside the tetrahedron counted positive,
- outer-circle outside the appropriate triangle and outer-sphere outside the tetrahedron counted positive, and
- one of them inside and the other one outside counted negative.
Combining the portions of the tetrahedrons which share the point  delivers the commonly used notation
delivers the commonly used notation
with 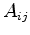 the Voronoi area of the edge
the Voronoi area of the edge
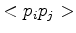 (coupling area between
(coupling area between  and
and 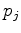 )
)
 |
(3.30) |
Equation (3.29) must be fulfilled for each grid point  inside the simulation domain, which results in an equation system
inside the simulation domain, which results in an equation system
with the system matrix
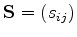
the unknowns
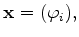 |
(3.34) |
and the right-hand side
which is defined for all inner points  of the domain.
of the domain.
For solving this time-invariant elliptical partial differential equation, boundary conditions have to be applied to all boundaries.
For each grid point lying at the boundary of the domain one of the two following additional equations or a linear-combination of them must be added for the discrete version, which fulfill the boundary conditions.
Each grid point of the boundary has to be defined by exactly one of the different conditions. Additionally, at least one grid point must be described by a Dirichlet condition to define a definite potential distribution.
With this set of equations, the discrete Poisson equation can be solved.
The first class of boundary conditions is an imposed potential 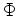
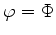 on boundary on boundary
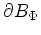 . . |
(3.36) |
The discrete formulation of this boundary condition simply replaces the respective rows of equation (3.29) by
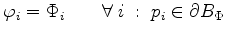 |
(3.37) |
or within the matrix representation
which at first delivers an asymmetric system matrix
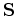 . Since most equation solvers require a symmetric system matrix, it may be necessary to transform the matrix to a symmetric one, which can be simple obtained by summation of adequate rows.
. Since most equation solvers require a symmetric system matrix, it may be necessary to transform the matrix to a symmetric one, which can be simple obtained by summation of adequate rows.
As shown in Section 2.3, for satisfying the maximum principle the system matrix
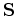 has to be an M-matrix. Under the precondition of a valid Delaunay grid, the validity of the M-matrix will be shown.
has to be an M-matrix. Under the precondition of a valid Delaunay grid, the validity of the M-matrix will be shown.
As the grid is Delaunay, it follows that the coupling areas are positive
and therefore,
and finally by defining at least one boundary point
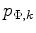 as a Dirichlet point
as a Dirichlet point
Figure 3.7:
A Voronoi box of the point  at a boundary.
at a boundary.
|
|
The second type of boundary condition specifies the imposed normal component
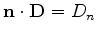 on the boundaries
on the boundaries
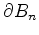 (see Figure 3.7), which occurs between different segments. As shown in Figure 3.7, the normal vector
(see Figure 3.7), which occurs between different segments. As shown in Figure 3.7, the normal vector
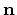 may have various directions on different boundary pieces around
may have various directions on different boundary pieces around  . This behavior could be handled by splitting the boxes (and also the point
. This behavior could be handled by splitting the boxes (and also the point  itself) into several pieces. Usually this approach is prevented and the normal derivatives are combined to one value.
In this case, the boundary conditions result in a distortion of (3.29)
itself) into several pieces. Usually this approach is prevented and the normal derivatives are combined to one value.
In this case, the boundary conditions result in a distortion of (3.29)
with 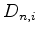 the assigned normal component at the boundary at the grid point
the assigned normal component at the boundary at the grid point  . It must be distinguished between
. It must be distinguished between 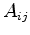 which represents the area of the Voronoi box between
which represents the area of the Voronoi box between  and
and 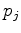 , and
, and 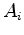 as the assigned boundary area of the Voronoi box around the grid point
as the assigned boundary area of the Voronoi box around the grid point  .
.
In the majority of cases, a special kind of this boundary condition is used, which shows a vanishing flux across the boundary (homogenous Neumann condition)
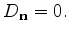 |
(3.42) |
This type of condition specifies the artificial boundaries which terminate the simulation domains.
As no distortion of equation (3.41) appears, these
boundaries do not require a special treatment and the equations can be left unchanged as in (3.31)-(3.35).
The linear-combination
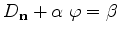 |
(3.43) |
combines the two previous conditions and results in the discrete formulation



Next: 3.2 The Diffusion Equation
Up: 3. The Box Integration
Previous: 3. The Box Integration
J. Cervenka: Three-Dimensional Mesh Generation for Device and Process Simulation
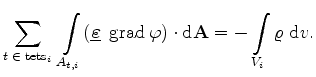
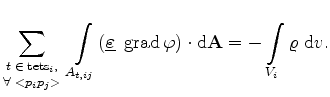
![\includegraphics[width=7cm]{htmlpicsconveps/newbox}](img234.png)
![\includegraphics[width=10cm]{picsconveps/kugel3}](img235.png)
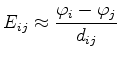 and
and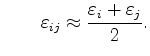
![\includegraphics[width=12cm]{htmlpicsconveps/tri3.eps}](img246.png)
![]() spans a local Cartesian coordinate system with origin
spans a local Cartesian coordinate system with origin ![]() .
In the one-dimensional case and with constant permittivity the potential varies linearly with position as
.
In the one-dimensional case and with constant permittivity the potential varies linearly with position as
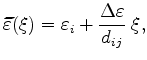
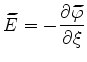
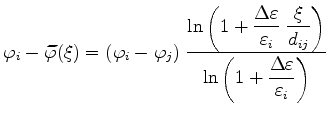
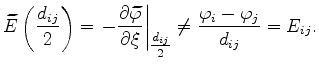
![\includegraphics[width=12cm, height=9cm]{picsconveps/reler}](img267.png)
![]() cause an additional contribution to the discretization error. With linear interpolation of
cause an additional contribution to the discretization error. With linear interpolation of
![]() and
and ![]() , equation (3.11) results in
, equation (3.11) results in
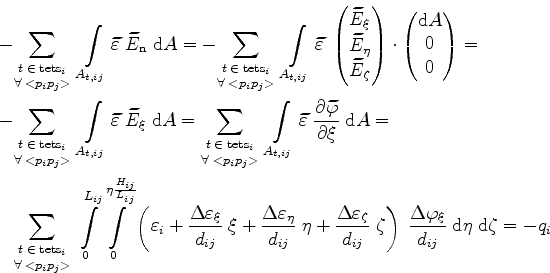
![]() is [27]
is [27]
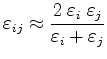

![]()
![]() . Since most equation solvers require a symmetric system matrix, it may be necessary to transform the matrix to a symmetric one, which can be simple obtained by summation of adequate rows.
. Since most equation solvers require a symmetric system matrix, it may be necessary to transform the matrix to a symmetric one, which can be simple obtained by summation of adequate rows.
![]() has to be an M-matrix. Under the precondition of a valid Delaunay grid, the validity of the M-matrix will be shown.
has to be an M-matrix. Under the precondition of a valid Delaunay grid, the validity of the M-matrix will be shown.
![]() on the boundaries
on the boundaries
![]() (see Figure 3.7), which occurs between different segments. As shown in Figure 3.7, the normal vector
(see Figure 3.7), which occurs between different segments. As shown in Figure 3.7, the normal vector
![]() may have various directions on different boundary pieces around
may have various directions on different boundary pieces around ![]() . This behavior could be handled by splitting the boxes (and also the point
. This behavior could be handled by splitting the boxes (and also the point ![]() itself) into several pieces. Usually this approach is prevented and the normal derivatives are combined to one value.
In this case, the boundary conditions result in a distortion of (3.29)
itself) into several pieces. Usually this approach is prevented and the normal derivatives are combined to one value.
In this case, the boundary conditions result in a distortion of (3.29)