 Gleichungen der Form
Gleichungen der Form 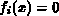 mit
mit  Unbekannten
Unbekannten 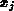 wird eine
wird eine 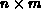 Matrix der
partiellen Ableitungen der
Matrix der
partiellen Ableitungen der  Gleichungen
Gleichungen 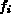 benötigt.
Ein Element
benötigt.
Ein Element 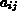 der Jacobi-Matrix ist zu
der Jacobi-Matrix ist zu
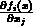 definiert.
definiert.




Bei der Berechnung der Lösung (der Nullstelle) eines nichtlinearen
Gleichungssystems bestehend aus  Gleichungen der Form
Gleichungen der Form 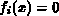 mit
mit  Unbekannten
Unbekannten 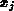 wird eine
wird eine 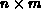 Matrix der
partiellen Ableitungen der
Matrix der
partiellen Ableitungen der  Gleichungen
Gleichungen 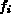 benötigt.
Ein Element
benötigt.
Ein Element 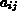 der Jacobi-Matrix ist zu
der Jacobi-Matrix ist zu
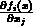 definiert.
definiert.
Die Elemente der Matrix können folgende Werte annehmen:
 :
:
 , d.h. diese Gleichung hängt nicht von
, d.h. diese Gleichung hängt nicht von 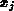 ab.
Die Jacobi-Matrix für typische elektrische Netzwerke hat nur 2 bis 3
ab.
Die Jacobi-Matrix für typische elektrische Netzwerke hat nur 2 bis 3
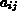 in einer Zeile, die ungleich
in einer Zeile, die ungleich  sind.
sind.
 . Insbesondere treten bei den partiellen
Ableitungen der Topologie-Gleichungen die Werte
. Insbesondere treten bei den partiellen
Ableitungen der Topologie-Gleichungen die Werte 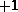 und
und 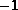 auf.
Andere typische Fälle sind die partiellen Ableitungen der
Gleichungen der Form
auf.
Andere typische Fälle sind die partiellen Ableitungen der
Gleichungen der Form 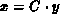 , die bei den idealen Bauelementen
(Widerstand, etc.) auftreten.
, die bei den idealen Bauelementen
(Widerstand, etc.) auftreten.
Die Berechnung der Jacobi-Matrix ist neben der Auswertung des Netzwerkgleichungssystems selber der zeitkritischste Teil während der Simulation, da dieser Teil in der innersten Schleife der Simulation - der Iteration zur Bestimmung der Lösungen der Netzwerkgleichungen zu einem bestimmten Zeitpunkt - durchgeführt wird. Daher muß der effizienten Berechnung der Jacobi-Matrix ein besonderes Augenmerk geschenkt werden.
In JANAP wird die Jacobi-Matrix in folgenden Schritten ermittelt:
 sind, werden überhaupt nicht in der
Matrix gespeichert. Die Jacobi-Matrix wird in Form einer schwach
besetzten Matrix (Sparse Matrix, [126][57][56][54][52][46])
gespeichert.
sind, werden überhaupt nicht in der
Matrix gespeichert. Die Jacobi-Matrix wird in Form einer schwach
besetzten Matrix (Sparse Matrix, [126][57][56][54][52][46])
gespeichert.
Bei der Ermittlung der Jacobi-Matrix ergibt sich ein Problem, das aus
der großen Flexibilität bei der Beschreibung des Netzwerkes in JANAP
resultiert.
Das Muster der Jacobi-Matrix, das ist das Muster der Elemente der
Matrix, die ungleich  sind, kann nicht a priori ermittelt werden, da
sich dieses Muster ändern kann (z.B. durch Öffnen oder Schließen eines
Schalters).
Es muß daher nach jeder Ermittlung der Jacobi-Matrix der variable Teil
der Matrix auf Elemente mit dem Wert
sind, kann nicht a priori ermittelt werden, da
sich dieses Muster ändern kann (z.B. durch Öffnen oder Schließen eines
Schalters).
Es muß daher nach jeder Ermittlung der Jacobi-Matrix der variable Teil
der Matrix auf Elemente mit dem Wert  überprüft werden.
überprüft werden.



