Im folgenden wird der prinzipielle Ablauf des Iterationsalgorithmus zur Bestimmung der Lösung des Gleichungssystems dargestellt.
Ein wichtiger Aspekt bei der Lösung eines nichtlinearen Gleichungssystems ist die Wahl des Startwertes für das Iterationsverfahren. Je nach Art der durchzuführenden Simulation wurde in JANAP eine der folgenden Methoden implementiert:
entspricht dem energielosen Zustand des Netzwerks.
Falls diese Wahl nicht zum gewünschten Ergebnis führt
(keine Konvergenz der Iteration oder Schaltung hat mehrere mögliche
Anfangszustände wie z.B. ein Flip-Flop), kann der Anwender mit
Hilfe der INITIAL-Anweisung (A.4.3.12) eigene Anfangswerte
vorgeben.
Wie bereits in Abschnitt 11.4.4 ausgeführt, wird die Jacobi-Matrix zum Großteil symbolisch ermittelt, sofern die Elemente nicht sowieso konstant sind.
Trotz dieser recht effizienten Methode zur Ermittlung der Jacobi-Matrix
ist der Rechenzeitbedarf immer noch relativ groß.
Nun geht das Iterationsverfahren davon aus, daß der Wert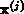 
bereits in der Nähe der Lösung liegt und es treten daher nur kleine
Änderungen von 
und damit der Jacobi-Matrix auf.
Aus diesem Grund wird die Jacobi-Matrix (und damit die Neuberechnung
der Skalierung und der Faktorisierung des Gleichungssystems) nicht jedesmal
neu ermittelt.
Dadurch ist natürlich die Konvergenzgeschwindigkeit nur mehr
linear, der Rechenzeitaufwand sinkt jedoch deutlich und infolge
der Nähe der Lösung gleichen die großen Iterationsschritte
die geringere Konvergenzgeschwindigkeit wieder aus.
Als Kriterium, wann die Jacobi-Matrix neu zu ermitteln ist, werden
die Normen der Fehler im Gleichungssystem 12.1
herangezogen.
Wenn die Bedingung
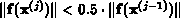erfüllt ist und keine Dämpfung notwendig war, wird die Jacobi-Matrix
nicht neu berechnet (Bypass).
Die Ausnahme, daß nach einer Dämpfung die Jacobi-Matrix auf alle
Fälle neu berechnet wird, ist erforderlich, da ja eine Dämpfung genau
dann durchgeführt wird, wenn die Änderung von groß ist und
daher die Jacobi-Matrix nicht mehr stimmen kann.
Die Jacobi-Matrix wird in Form von drei Feldern gespeichert. Die drei Felder sind:
NZ Speicherzellen, wobei
NZ die Anzahl der Elemente der Jacobi-Matrix ist, die
strukturell ungleich 0 sind (d.h. ungleich 0 sind oder in einem
bestimmten Zustand ungleich 0 sein können).
Da die zur Lösung des linearen Gleichungssystems verwendeten
Routinen (MA28) nicht erfordern, daß die Jacobi-Matrix
spalten- oder zeilenweise sortiert sein muß, wird die Jacobi-Matrix
unsortiert, bestehend aus drei Blöcken, erstellt. Diese drei
Blöcke sind:
Die Gleichungen im Gleichungssystem 12.1 enthalten
Gleichungen mit Faktoren in sehr unterschiedlichen Größenordnungen.
Zur Illustration sei die einfache Parallelschaltung eines
Kondensators mit 1nF mit einem Widerstand von 1k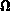
,
wie in Abbildung 12.1 dargestellt, angeführt.
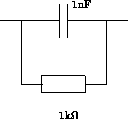
Abbildung 12.1: Parallelschaltung von Kapazität und Widerstand
Diese beiden Bauelemente resultieren unter anderem in den folgenden Gleichungen im Gleichungssystem:
In beiden Gleichungen kommt die gemeinsame Spannung 
vor, wobei jedoch
die Faktoren von um den Faktor 
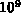auseinander liegen.
Bei den gängigen Rechnern (IBM 370-Architektur, Vax-Architektur)
haben die Mantissen bei einfacher Genauigkeit nur knapp mehr als 7
Dezimalstellen.
Die Kapazität hat daher in Relation zum Widerstand den Wert 0.
Zur Bewertung des Iterationswertes 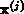wird die
Norm der Residuen des Gleichungssystems 12.1 herangezogen.
Wenn nun die gleiche Größe in unterschiedlichen Gleichungen mit
extrem verschiedenen Faktoren eingeht, bedeutet dies, daß aufgrund einer
Gleichung der Wert von bereits genau genug erreicht sein kann,
obwohl die andere Gleichung nicht im geringsten erfüllt ist.
Um dieses Mißverhältnis zu mildern, wird eine Skalierung der Gleichungen nach folgenden Verfahren vorgenommen:
In diesem Gleichungssystem sind die Faktoren von nur mehr um den
Faktor 
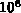auseinander. Dadurch wird die Genauigkeit der Endlösung
des Iterationsverfahrens verbessert.
Die zentrale Aufgabe ist neben der Berechnung der Jacobi-Matrix die Lösung des Gleichungssystems
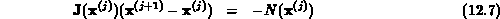
Bei der Auswahl des Verfahrens zur Lösung des linearen Gleichungssystems 12.7 müssen folgende Eigenschaften der Jacobi-Matrix berücksichtigt werden:
Für JANAP werden die von Iain S. Duff für die Britische Atomenergie Behörde A.E.R.E in Harwell entwickelte Routinen MA28 verwendet. Die in den Routinen verwendeten Algorithmen sind in [125][102][58][55][53][52][49][48][47][45] dokumentiert.
Die Routinen bestehen im wesentlichen aus drei Unterprogrammen, die vom Benutzer aufgerufen werden und 10 weiteren intern verwendeten Unterprogrammen. Die von JANAP direkt aufgerufenen Routinen sind:
In der folgenden Tabelle wird die Größenordnung des Rechenzeitbedarfs
der einzelnen Routinen dargestellt [53].
Im Vergleich dazu wird der
Rechenzeitbedarf des Lösens des Gleichungssystems ohne Berücksichtigung
der speziellen Eigenschaften der Jacobi-Matrix angeführt [25].
(Annahme: 3 Elemente ungleich 0 in einer Zeile, Rang 
, Fillin-Faktor 2)
Aus dieser Aufstellung ist deutlich der Vorteil der Sparse-Matrix Techniken für große Matrizen ersichtlich. Dieser Vorteil ist auch gegeben, obwohl die Methoden der kompakten Speicherung der Matrix natürlich einen wesentlich größeren Verwaltungsaufwand erfordern.
Durch die Verwendung der alten Jacobi-Matrix, sofern sie sich nicht essentiell verändert hat, sinkt die Rechenzeit um den Faktor 9. Wenn sich nur die Werte der Matrix, nicht aber die Plätze der Werte ungleich 0, geändert haben, sinkt die Rechenzeit um einen Faktor 2.
An Hand der in Abbildung 12.2 graphisch dargestellten funktionalen Abhängigkeit des Stromes von der Spannung in einer einfachen Schaltung, bestehend aus einer Diode, die über einen Widerstand von einer Spannungsquelle gespeist wird, läßt sich die Notwendigkeit einer Dämpfung erkennen.
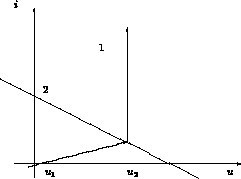
Abbildung 12.2: Überschießen der Iteration
Kurve 1 stellt die Kennlinie der Diode, Kurve 2 die Kennlinie der
Serienschaltung aus Spannungsquelle und Widerstand dar.
Wenn nun die Iteration bei der Span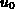nung 
beginnt und eine Tangente
an Kurve 1 - die Kurve einer Exponentialfunktion - gelegt wird,
um den nächsten Iterationswert zu erhalten, ergibt sich als
Schnittpunkt zwischen Tangente und Kurve 2 die Spannung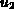 
.
Wenn nun für 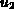der Strom durch die Diode bestimmt werden soll,
ist dies praktisch nicht mehr möglich, da dieser wegen der großen
Steigung der Kurve 1 über alle Grenzen wächst.
Mit einem derartigen Verhalten muß bei allen nichtlinearen Gleichungssystemen, die die Exponentialfunktion enthalten, gerechnet werden. Bei der Simulation von elektrischen Netzwerken tritt in allen realistischen Modellen der bipolaren Halbleiterbauelemente die Exponentialfunktion in zentraler Stelle auf. Es müssen daher geeignete Maßnahmen getroffen werden, um das Überschießen zu mildern. Die generell angewandte Methode ist die Beschränkung der Schrittweite des Newton-Verfahrens. Die meisten Netzwerkanalyseprogramme, die fix eingebaute Halbleiterbauelementmodelle verwenden, haben diese Modelle dahingehend modifiziert (durch entsprechende Begrenzung von einzelnen Werten), daß die gröbsten Probleme vermieden werden können. JANAP hat aus Gründen der Flexibilität der Modellbildung keine eingebauten Modelle. Daher können diese nicht modifiziert werden und die kritischen Stellen auch nicht trivial erkannt werden. JANAP verwendet zwei Methoden zur Verhinderung des Überschießens:
In JANAP wird eine adaptive Dämpfung nach Bank/Rose [7][6] eingesetzt.
Die Grundidee dieses Verfahrens ist, daß die Gleichung 12.7 durch Gleichung 12.8 ersetzt wird:
oder anders ausgedrückt, wird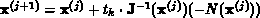 
als neuer
-Wert verwendet, wobei der Dämpfungsparameter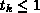 
gewählt wird.
Der Fall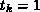 
entspricht keiner Dämpfung.
In [7] wird gezeigt, daß mit diesem Verfahren eine
quadratische Konvergenz der Iteration erreicht werden kann.
Der praktische Dämpfungs-Algorithmus hat, grob dargestellt, folgenden Ablauf:
Zur Feststellung, ob dx schon zu klein für eine Dämpfung geworden ist, werden zwei Kriterien verwendet:
dxqxn (relativer Abstand zwischen 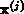und
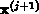) ist kleiner als die fünffache geforderte
relative Genauigkeit.
dxqxn ist kleiner als die geforderte
relative Genauigkeit.
Ein wichtiges Element jedes Iterationsverfahrens ist die Entscheidung, ob die gewünschte Genauigkeit erreicht worden ist und daher das Iterationsverfahren beendet werden kann.
Das einzig richtige Kriterium ist die Feststellung der Abweichung des monentanen Iterationswertes von der Lösung des Gleichungssystems. Dieses Kriterium kann leider nicht verwendet werden, da ja die Lösung nicht bekannt ist, sondern berechnet werden soll. Es müssen daher andere Kriterien herangezogen werden, die einerseits auf der Größe des Residuums aufbauen und andererseits die Geschwindigkeit der Konvergenz verwenden. In JANAP werden die folgenden Kriterien eingesetzt:
dxqxn
(relativer Abstand zwischen 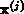und )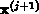
kleiner als die geforderte relative Genauigkeit ist.
dxqxn kleiner als die Hälfte
dieses Wertes bei der letzten Iteration sein.
PARAM-Anweisung in der JANAP-Eingabe
geändert werden.
Zur Bestimmung der Norm eines Vektors wird die Euklidische Norm(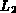
)
verwendet.
Für die Norm zur Bestimmung des relativen Abstands zwischen zwei Vektoren
und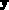 
wird folgende Formel verwendet [123]:
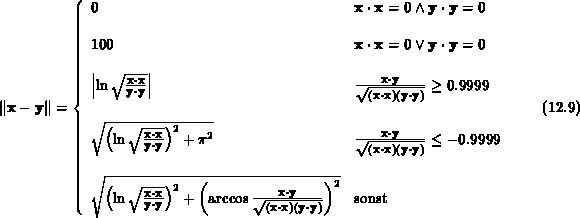
Der Wert 100 für den Fall, daß nur einer der beiden Vektoren null ist,
entspricht der Norm für die Vektoren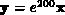 
- einer guten Annäherung von unendlich.
Fal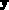ls als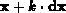 
(
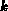ist eine reelle
Zahl) gegeben ist, werden die inneren Produkte mit 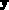nach den
Formeln
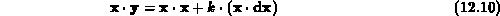
und
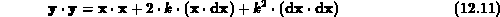
ermittelt.
Während der Dämpfung des Newton-Verfahrens wird nur 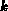verändert.
Durch diese Berechnungsmethode sind die inneren Produkte
, 
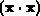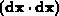und
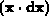nur einmal zu berechnen.
Dadurch ergibt sich eine deutliche Reduktion der Rechenzeit.