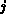 des
des  -Pols wird eine ``virtuelle Ladung''
-Pols wird eine ``virtuelle Ladung''
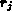 nach folgenden Regeln zugeordnet:
nach folgenden Regeln zugeordnet:




Jedem Anschluß 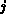 des
des  -Pols wird eine ``virtuelle Ladung''
-Pols wird eine ``virtuelle Ladung''
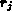 nach folgenden Regeln zugeordnet:
nach folgenden Regeln zugeordnet:
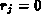 , wenn der Strom des Anschlusses nur in einer Gleichung der Form
, wenn der Strom des Anschlusses nur in einer Gleichung der Form
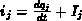 vorkommt.
vorkommt.
somit ist auch
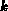 Anschlüsse münden, gilt:
Anschlüsse münden, gilt:
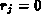 gibt an, daß das Bauteil keine Ladung von der Anode zur Kathode
bzw. umgekehrt durchläßt.
gibt an, daß das Bauteil keine Ladung von der Anode zur Kathode
bzw. umgekehrt durchläßt.
Die verallgemeinerte Knotenregel für Ladungen lautet nun:
Für jeden Knoten eines Netzwerkes ist die Summe der realen und virtuellen Ladungenüber alle Anschlüsse summiert, die in den Knoten münden, gleich
.
Das Gleichungssystem für diese Regel lautet:
wobei 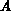 die Koeffizientenmatrix der 1. Kirchhoff'schen Regel ist.
die Koeffizientenmatrix der 1. Kirchhoff'schen Regel ist.
Es ist zu beachten, daß die 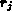 nicht in allen Fällen (z.B. bei
einem Netzwerk, das nur aus Spannungsquellen und Widerständen besteht)
berechnet werden kann. Dies ist ungewöhnlich aber nicht störend, da
die
nicht in allen Fällen (z.B. bei
einem Netzwerk, das nur aus Spannungsquellen und Widerständen besteht)
berechnet werden kann. Dies ist ungewöhnlich aber nicht störend, da
die 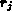 ja nur helfen sollen, eine einfache Beschreibung des
Netzwerks zu erhalten. Die konkreten Werte werden nicht benötigt.
Die Werte sind jedoch durch die Anfangsbedingungen (0) definiert.
ja nur helfen sollen, eine einfache Beschreibung des
Netzwerks zu erhalten. Die konkreten Werte werden nicht benötigt.
Die Werte sind jedoch durch die Anfangsbedingungen (0) definiert.
Die Regel 7.3 kann leicht anhand des Beispiels in Abbildung 7.1 auf die in 5.3 abgeleitete Ladungsregel für die äußeren Kondensatoren zurückgeführt werden.
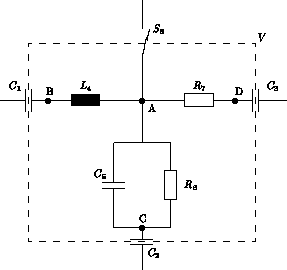
Abbildung 7.1: Kapazitiver Stern
Beim Übergang von n-Polen zu Zweipolen reicht eine virtuelle Ladung für jedes Bauteil aus. Die Zählpfeilrichtung wird wie für die realen Ladungen gewählt.
Wir haben für das Volumen 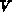 eine Ladungsregel, welche
die gespeicherten Ladungen in den Platten der drei
Kondensatoren an der Oberfläche des Volumens
eine Ladungsregel, welche
die gespeicherten Ladungen in den Platten der drei
Kondensatoren an der Oberfläche des Volumens 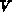 enthält.
enthält.
Aufgrund obiger Definition (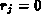 für Kondensatoren) können
wir Gleichung (7.5) abwandeln.
für Kondensatoren) können
wir Gleichung (7.5) abwandeln.
Der offene Schalter 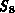 entspricht einem Leitwert mit Leitfähigkeit
0 und
entspricht einem Leitwert mit Leitfähigkeit
0 und 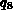 ist als 0 definiert.
ist als 0 definiert.
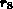 ist nicht definiert, wobei im energielosen Zustand der Wert 0
festgelegt wird.
Wir können nun den Schalter
ist nicht definiert, wobei im energielosen Zustand der Wert 0
festgelegt wird.
Wir können nun den Schalter 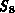 in Gleichung (7.6) einfügen
und erhalten (7.7):
in Gleichung (7.6) einfügen
und erhalten (7.7):
Gleichung (7.7) kann in folgende Form umgeschrieben werden:
Gleichung (7.8) ist für Knoten, in die nur Kondensatoren und offene
Schalter (oder Leitwerte mit Wert 0) münden,
aufgrund der Ladungsregel (5.9) und obiger Definitionen
gültig.
Es soll nun bewiesen werden, daß Gleichung (7.8)
für jeden Knoten der Schaltung gültig ist.
Der Beweis kann leicht anhand der Schaltung in Abbildung 7.1
nachvollzogen werden.
Es soll gezeigt werden, daß die Gleichung für Knoten 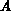 richtig ist.
Für die Knoten
richtig ist.
Für die Knoten 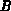 ,
, 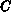 und
und 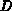 resultiert die Regel (7.8)
in die folgenden zusätzlichen Gleichungen:
resultiert die Regel (7.8)
in die folgenden zusätzlichen Gleichungen:
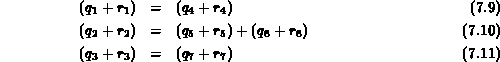
Durch Substitution dieser drei Gleichungen in Gleichung (7.7) erhält man Gleichung (7.12).
Gleichung (7.12) ist exakt die Regel (7.8) für
Knoten 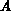 .
Damit ist gezeigt, daß Gleichung (7.8) für jeden Knoten
des elektrischen Netzwerks gültig ist.
.
Damit ist gezeigt, daß Gleichung (7.8) für jeden Knoten
des elektrischen Netzwerks gültig ist.
In den obigen Gleichungen wurde angenommen, daß Schalter 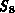 offen ist.
Das Volumen
offen ist.
Das Volumen 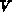 hat daher keine leitende Verbindung zur Umgebung und zu
möglichen Energiequellen.
Als nächstes soll nun der Fall behandelt werden,
wenn Schalter
hat daher keine leitende Verbindung zur Umgebung und zu
möglichen Energiequellen.
Als nächstes soll nun der Fall behandelt werden,
wenn Schalter 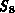 geschlossen ist oder war.
Gleichung (7.5) für Volumen
geschlossen ist oder war.
Gleichung (7.5) für Volumen 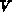 muß in der Form
(7.13) umgeschrieben werden, wobei
muß in der Form
(7.13) umgeschrieben werden, wobei 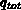 die gesamte Ladung,
die in das Volumen
die gesamte Ladung,
die in das Volumen 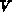 eingebracht wurde, symbolisiert.
eingebracht wurde, symbolisiert.
Durch Vergleich der Gleichungen (7.13) und (7.7) ergibt sich die Beziehung
Da 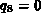 für den Schalter definiert ist, kann (7.14) vereinfacht
werden:
für den Schalter definiert ist, kann (7.14) vereinfacht
werden:
Aufgrund von Gleichung (7.15) kann der Wert von 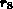 als die
gesamte Ladung, die in Volumen
als die
gesamte Ladung, die in Volumen 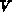 eingebracht wurde, betrachtet werden.
Verallgemeinert kann gesagt werden:
eingebracht wurde, betrachtet werden.
Verallgemeinert kann gesagt werden:
Die Summe der virtuellen Ladungen der Elemente an der Oberfläche eines Volumens repräsentieren die Gesamtladung, die in das Volumen eingebracht wurde oder dem Volumen entzogen wurde.
Zum Abschluß der Diskussion der erweiterten Ladungsregel ist noch
die Definition 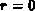 für Stromquellen zu begründen.
Diese Festlegung kann am besten anhand einer einfachen Schaltung, die
aus einer Stromquelle zu der ein Kondensator parallel geschaltet ist,
motiviert werden.
Aufgrund der physikalischen Gesetze ist dies keine zulässige
Schaltung, wenn die Stromquelle einen Strom ungleich 0 einprägt.
Wenn wir die erweiterte Ladungsregel (7.8) für einen der
beiden Knoten der Schaltung aufstellen, erhalten wir die Gleichung
für Stromquellen zu begründen.
Diese Festlegung kann am besten anhand einer einfachen Schaltung, die
aus einer Stromquelle zu der ein Kondensator parallel geschaltet ist,
motiviert werden.
Aufgrund der physikalischen Gesetze ist dies keine zulässige
Schaltung, wenn die Stromquelle einen Strom ungleich 0 einprägt.
Wenn wir die erweiterte Ladungsregel (7.8) für einen der
beiden Knoten der Schaltung aufstellen, erhalten wir die Gleichung
Durch Einsetzen der definierten Werte von  und
und 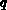 wird Gleichung
(7.16) vereinfacht:
wird Gleichung
(7.16) vereinfacht:
Die Bauelement-Gleichungen des Kondensators sind:
Durch Einsetzen der Bauelement-Gleichung der Stromquelle und Integration von Gleichung (7.18) erhält man
Vergleicht man Gleichung (7.17) mit (7.20) ergibt sich die Beziehung (7.21).
Diese Beziehung ist nur unter zwei Bedingungen erfüllt:



