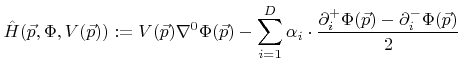 |
(3.12) |
To solve the LS equation for non-convex Hamiltonians the Lax-Friedrichs scheme can be applied [87,110]. Some artificial dissipation is introduced to obtain stability. The approximation to the Hamiltonian for this scheme is written as
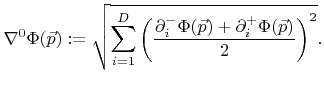 |
(3.13) |
The constants
![]() are dissipation coefficients which should fulfill
are dissipation coefficients which should fulfill
The choice of these dissipation coefficients is the main problem for the applicability of this scheme. Larger values lead to unnecessary smoothing of the surface, while smaller values cause numerical instabilities. The analytical evaluation of the right-hand side in (3.14) to find the optimal values for the constants
![]() is usually not possible for general surface velocities. However, often the optimal values cannot be straightforwardly evaluated, because the velocity field may depend on the particle transport which further depends on the surface geometry. Hence, the likely best way to find the optimal values is to test different values and analyze the results [98].
is usually not possible for general surface velocities. However, often the optimal values cannot be straightforwardly evaluated, because the velocity field may depend on the particle transport which further depends on the surface geometry. Hence, the likely best way to find the optimal values is to test different values and analyze the results [98].