Next: 4.6 Multiple Material Regions
Up: 4. A Fast Level
Previous: 4.4.3 Pattern Transfer
4.5 Smoothing
The LS method also provides a simple way to smooth a given geometry. Setting the surface velocity in the LS equation equal to the mean curvature leads to a smoothed surface [110]. The definition of the mean curvature and its approximation were given in Section 3.3.2. The introduction of a lower limit
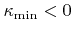 and an upper limit
and an upper limit
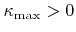 for regions with negative and positive curvature, respectively, controls the amount of smoothing. The smoothing algorithm is realized by setting the surface velocity field as follows
for regions with negative and positive curvature, respectively, controls the amount of smoothing. The smoothing algorithm is realized by setting the surface velocity field as follows
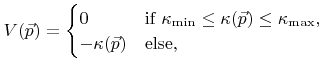 |
(4.17) |
and solving the LS equation over time until all surface velocities are equal to 0. Figure 4.7 demonstrates smoothing for the test structure given in Figure 4.5 with
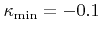 and
and
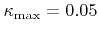 .
.
Figure 4.7:
The final surface after a smoothing operation is applied to the geometry given in Figure 4.5a. The curvature is limited by
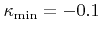 and
and
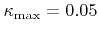 .
.
|
|




Next: 4.6 Multiple Material Regions
Up: 4. A Fast Level
Previous: 4.4.3 Pattern Transfer
Otmar Ertl: Numerical Methods for Topography Simulation
![]() and an upper limit
and an upper limit
![]() for regions with negative and positive curvature, respectively, controls the amount of smoothing. The smoothing algorithm is realized by setting the surface velocity field as follows
for regions with negative and positive curvature, respectively, controls the amount of smoothing. The smoothing algorithm is realized by setting the surface velocity field as follows