



Next: 5.3.2 Coned Cosine Distribution
Up: 5.3 Generation of Random
Previous: 5.3 Generation of Random
First the power cosine distribution as introduced in (2.6) is considered, where
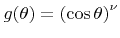 with
with 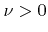 . Thus the probability density function for the polar angle is given as
. Thus the probability density function for the polar angle is given as
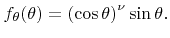 |
(5.36) |
Calculating the cumulative distribution function results in
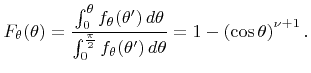 |
(5.37) |
A variate obeying an arbitrary distribution can be obtained using the inversion method [25]. A uniformly distributed variate  on
on
![$ \left[0,1\right]$](img715.png) mapped by the inverse cumulative distribution function leads to the desired distribution [115]
mapped by the inverse cumulative distribution function leads to the desired distribution [115]
![$\displaystyle {\theta}={F}_{\theta}^{-1}({u})=\arccos\left(\sqrt[{\nu}+1]{1-{u}}\right).$](img716.png) |
(5.38) |
Since 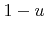 is uniformly distributed on
is uniformly distributed on
![$ \left[0,1\right]$](img715.png) as well, the random polar angle can also be generated by [66]
as well, the random polar angle can also be generated by [66]
![$\displaystyle {\theta}=\arccos\left(\sqrt[{\nu}+1]{{u}}\right).$](img718.png) |
(5.39) |
Algorithm 5.2 summarizes the generation of a random polar angle following the probability density function (5.36).
![\begin{algorithm}
% latex2html id marker 9424\caption{Generation of a $\left(\...
...turn $\sqrt[{\nu}+1]{\funcrand ()}$\ instead.
\end{algorithmic}}
\end{algorithm}](img719.png)




Next: 5.3.2 Coned Cosine Distribution
Up: 5.3 Generation of Random
Previous: 5.3 Generation of Random
Otmar Ertl: Numerical Methods for Topography Simulation
![]() with
with ![]() . Thus the probability density function for the polar angle is given as
. Thus the probability density function for the polar angle is given as
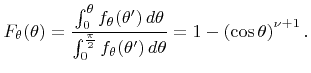
![]() on
on
![]() mapped by the inverse cumulative distribution function leads to the desired distribution [115]
mapped by the inverse cumulative distribution function leads to the desired distribution [115]