



Next: 5.3.1 Power Cosine Distribution
Up: 5. Surface Rate Calculation
Previous: 5.2.10 Benchmarks
The generation of random directions is essential for the Monte Carlo based calculation of particle transport. It is difficult to find instructions for the generation of random directions which obey a certain angular distribution, except for uniform spherical [92] or cosine distributions [37]. Therefore, recipes for the generation of variate distributions used in this work are given in the following discussion.
The arrival directions of particles at the source plane
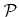 and the directions of reemitted particles are usually described by probability densities
and the directions of reemitted particles are usually described by probability densities
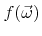 , which only depend on the polar angle
, which only depend on the polar angle 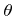 relative to a certain direction
relative to a certain direction 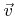
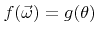 with with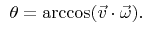 |
(5.33) |
Using spherical coordinates with respect to 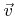 the probability density function can be formulated as
the probability density function can be formulated as
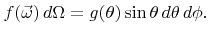 |
(5.34) |
Since this expression is separable, the azimuthal angle 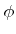 and the polar angle
and the polar angle 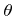 are independent, which allows for the description of both variables by individual probability densities
are independent, which allows for the description of both variables by individual probability densities
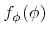 and
and
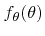
The probability density function
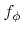 is constant, which is a direct consequence of the rotational symmetry of the directional distribution. Therefore, since the azimuthal angle is uniformly distributed on
is constant, which is a direct consequence of the rotational symmetry of the directional distribution. Therefore, since the azimuthal angle is uniformly distributed on
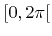 , a random choice of
, a random choice of 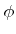 is trivial. Picking a random polar angle is more sophisticated. In the following sections algorithms are presented for selecting a polar angle according to directional distributions which are frequently used for the description of arrival or reemission angles.
is trivial. Picking a random polar angle is more sophisticated. In the following sections algorithms are presented for selecting a polar angle according to directional distributions which are frequently used for the description of arrival or reemission angles.
Subsections




Next: 5.3.1 Power Cosine Distribution
Up: 5. Surface Rate Calculation
Previous: 5.2.10 Benchmarks
Otmar Ertl: Numerical Methods for Topography Simulation
![]() and the directions of reemitted particles are usually described by probability densities
and the directions of reemitted particles are usually described by probability densities
![]() , which only depend on the polar angle
, which only depend on the polar angle ![]() relative to a certain direction
relative to a certain direction ![]()