Next: 3.4 Local Oxidation Nanolithography Up: 3.3 Nitric Acid Oxidation Previous: 3.3 Nitric Acid Oxidation
In order to model NAOS, experimental results from several publications from the group of Asuha et al. at the Institute of Scientific and Industrial Research at Osaka University and from Imai at al. at the Display Technology Development Group at Sharp Corporation are analyzed [88], [89], [103].
The phase diagram of the HNO
For the azeotropic NAOS method the silicon substrate is submerged in a nitric acid (HNO![]() ) liquid at its boiling temperature. The method is
usually performed with a 61wt% concentration of HNO
) liquid at its boiling temperature. The method is
usually performed with a 61wt% concentration of HNO![]() at the boiling temperature of 112
at the boiling temperature of 112
![]() C. An alternative is a 68wt% concentration
(location C in Figure Figure 3.7), at the boiling temperature of 120.7
C. An alternative is a 68wt% concentration
(location C in Figure Figure 3.7), at the boiling temperature of 120.7
![]() C. The chemical reaction which
takes place in order to generate the oxygen required for the oxidation process is
C. The chemical reaction which
takes place in order to generate the oxygen required for the oxidation process is
| (94) |
The maximum thicknesses of SiO![]() reached
are 1.2nm and 1.4nm by oxidation with 61wt% and 68wt% HNO
reached
are 1.2nm and 1.4nm by oxidation with 61wt% and 68wt% HNO![]() , respectively within 10 minutes, while prolonged oxidation does not increase the
SiO
, respectively within 10 minutes, while prolonged oxidation does not increase the
SiO![]() thickness. However, until the final thickness is reached, there is still a time dependence on the immersed oxide thickness.
This is shown in Figure 3.8a where the thickness of the NAOS oxide is plotted with respect to the immersion time at
an ambient temperature of 25
thickness. However, until the final thickness is reached, there is still a time dependence on the immersed oxide thickness.
This is shown in Figure 3.8a where the thickness of the NAOS oxide is plotted with respect to the immersion time at
an ambient temperature of 25
![]() C immersed in a 61wt% HNO
C immersed in a 61wt% HNO![]() solution.
Similarly, the temperature dependence on oxide thickness is shown in Figure 3.8b. The thicknesses obtained are after
immersion for 10 minutes in a 61wt% HNO
solution.
Similarly, the temperature dependence on oxide thickness is shown in Figure 3.8b. The thicknesses obtained are after
immersion for 10 minutes in a 61wt% HNO![]() solution. At the final experimental dot, at a temperature of 112
solution. At the final experimental dot, at a temperature of 112
![]() C, the oxide reaches its
maximum thickness of 1.3nm within the 10 minutes provided.
C, the oxide reaches its
maximum thickness of 1.3nm within the 10 minutes provided.
|
The model must take into account both the influence of immersion time and temperature. From observing Figure 3.8, a linear-parabolic type of relationship seems to dominate the NAOS type of oxidation. The presented model proceeds to fit the experimental data into the linear-parabolic model for the oxide rate
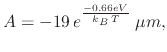 |
(96) |
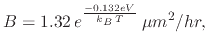 |
(97) |
The vapor NAOS oxidation method should be performed at temperatures above 200![]() C when the Nitric acid HNO
C when the Nitric acid HNO![]() is in a vapor phase.
The chemical reaction which takes place in order to generate the oxygen required for the oxidation reaction is
is in a vapor phase.
The chemical reaction which takes place in order to generate the oxygen required for the oxidation reaction is
| (99) |
In Figure 3.9 the thickness of the SiO![]() layer is plotted as a function of oxidation time for various
temperatures (300
layer is plotted as a function of oxidation time for various
temperatures (300
![]() C, 400
C, 400
![]() C, 450
C, 450
![]() C, and 500
C, and 500
![]() C).
At these temperatures, thermal oxidation would not be able to grow layers
larger than the native oxide due to the oxidants not having enough energy to diffuse through the oxide network.
The oxide thickness appears to increase with increased time; however the oxidation rate tends to decrease. This parabolic
relationship suggests that the diffusion of oxygen atoms through the growing oxide is the rate-determining step.
C).
At these temperatures, thermal oxidation would not be able to grow layers
larger than the native oxide due to the oxidants not having enough energy to diffuse through the oxide network.
The oxide thickness appears to increase with increased time; however the oxidation rate tends to decrease. This parabolic
relationship suggests that the diffusion of oxygen atoms through the growing oxide is the rate-determining step.
![\includegraphics[width=\linewidth]{chapter_process_modeling/figures/NAOS.eps}](img405.png) |
An empirical model which is to follow the oxide growth due to vapor NAOS oxidation must take into account the temperature and time dependence on the oxide thickness. At first the relationship between the oxide thickness and oxidation time is shown to be logarithmic
| (100) |
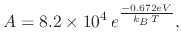 |
(101) |
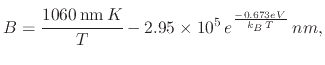 |
(102) |