Next: 4.1.4 Precursor Decomposition Up: 4.1 Spray Pyrolysis Deposition Previous: 4.1.2 Atomization Procedure
After the droplet leaves the atomizer, it travels through the ambient with an initial velocity determined by the atomizer. In the aerosol form, the droplets are transported with the aim of as many droplets as possible reaching the surface. As the droplets move through the ambient, they experience physical and chemical changes depicted in Figure 4.4.
|
As the droplet traverses the ambient, there are four forces simultaneously acting on it, describing its path. Those forces are gravitational,
electrical, thermophoretic, and the Stokes force. As shown in Figure 4.4, the droplets experience evaporation during their flight,
which affects the influence of the forces on their trajectory. Some experimental results from [121] indicate that solid particles
could form, when the reactor temperature is low, when the precursor solution concentration is high, and when the flow rate
of the carrier gas (N![]() ) is low.
) is low.
The gravitational force is the force pulling the droplet downward. The size of the force depends on the mass of the traveling droplet, which is a function of its volume and its density. The force is given by
The electrical force is applicable to spray pyrolysis systems which include an additional electrical source governing the droplet's trajectory. When an air blast atomizer is used, high speed air is the cause of atomization and aerosol production. Ultrasonic atomizers are electrically driven, whereby an electric generator is vibrated at ultrasonic frequencies through a titanium nozzle. Increasing the frequency can result in smaller droplet sizes. ESD atomizers use a strong electric force at the liquid-gas interface to generate charged droplets. Therefore, air blast atomizers do not have additional contributions from an electrical force and the droplet transport is driven by the gravitational force and the initial velocity, while for spray pyrolysis deposition using ultrasonic and ESD atomizers, the electrical force is the main component which drives the droplets downwards. The electrical force acting on a droplet is usually several orders of magnitude larger than the gravitational force and is given by
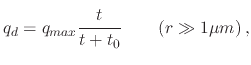 |
(154) |
The stokes force is the drag experienced by the droplet due to the air resistance in the ambient. Because of the spherical shape and small size of the droplet, the Stokes force is not equivalent to the force experienced by an irregularly shaped body. The force is caused by the friction between the droplet and air molecules. The Stokes force is a factor of the particle's velocity and size. Therefore, large droplets which move with a high velocity will experience the largest retarding force according to
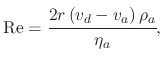 |
(157) |
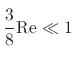 ),
it is often excluded from Stokes force calculations.
),
it is often excluded from Stokes force calculations.
The thermophoretic force is a retarding force, causing droplets to significantly decrease their velocity as they approach
the heated substrate. Figure 4.5 shows the temperature distribution near a heated substrate. The results for
the 210![]() C, 250
C, 250![]() C, and 310
C, and 310![]() C are taken from [171], while the results for the 400
C are taken from [171], while the results for the 400![]() C are from [64].
It is evident that the air temperature increases steeply due to the forced convection cooling effect of the air flow when close
to the heated substrate. Because the thermophoretic force depends on the thermal gradient in the transport environment, it
can be concluded that it will have no effect on the droplet movement, when it is several (
C are from [64].
It is evident that the air temperature increases steeply due to the forced convection cooling effect of the air flow when close
to the heated substrate. Because the thermophoretic force depends on the thermal gradient in the transport environment, it
can be concluded that it will have no effect on the droplet movement, when it is several (![]() 5-7) mm away from the substrate.
However, in this high thermal gradient region, the thermophoretic force begins to dominate. This is true for
PSD systems where the main
driving force is gravity; however, for ESD systems, the electrical force is often stronger than the thermophoretic force.
Therefore, the motion of the droplet within the ``thermal zone'' would not change significantly, but the
increased temperature would have other effects on the droplet, such as a reduction in size due to droplet evaporation in the region.
5-7) mm away from the substrate.
However, in this high thermal gradient region, the thermophoretic force begins to dominate. This is true for
PSD systems where the main
driving force is gravity; however, for ESD systems, the electrical force is often stronger than the thermophoretic force.
Therefore, the motion of the droplet within the ``thermal zone'' would not change significantly, but the
increased temperature would have other effects on the droplet, such as a reduction in size due to droplet evaporation in the region.
![\includegraphics[width=\linewidth]{chapter_process_technologies/figures/gradient.eps}](img578.png) |
The equation governing the strength of the thermophoretic force is given by
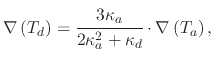 |
(159) |