Next: 6.5 BiCS Memory Hole Up: 6.4 Spray Pyrolysis Deposition Previous: 6.4.1 YSZ Deposition using
The deposition of tin oxide (SnO![]() ) on silicon dioxide using the spray pyrolysis deposition process was performed
by one of our industrial partners using an air atomizer which is not located directly above the wafer, but rather on
the side, as depicted in Figure 6.18.
) on silicon dioxide using the spray pyrolysis deposition process was performed
by one of our industrial partners using an air atomizer which is not located directly above the wafer, but rather on
the side, as depicted in Figure 6.18.
![\includegraphics[width=\linewidth]{chapter_applications/figures/AITspray.eps}](img847.png) |
As an example, a particle with a 5![]() m radius is analyzed. Its initial velocity is assumed to be 20m
m radius is analyzed. Its initial velocity is assumed to be 20m![]() s, fully in the horizontal direction.
Therefore, the only forces which the particle experiences are the gravitational force and the Stokes force during its vertical flight and the Stokes force during its
lateral flight towards the wafer sample. The droplet's vertical downward acceleration due to gravity is given by 9.81m
s, fully in the horizontal direction.
Therefore, the only forces which the particle experiences are the gravitational force and the Stokes force during its vertical flight and the Stokes force during its
lateral flight towards the wafer sample. The droplet's vertical downward acceleration due to gravity is given by 9.81m![]() s
s![]() . The Stokes force is
given by (4.7) and for the sample droplet is valued at 2.07
. The Stokes force is
given by (4.7) and for the sample droplet is valued at 2.07![]() 10
10
![]() N. The mass of the droplet is given by
(4.2) and is calculated to 523
N. The mass of the droplet is given by
(4.2) and is calculated to 523![]() 10
10![]() kg. Therefore, the negative acceleration due to the stokes force is approximately
3960
kg. Therefore, the negative acceleration due to the stokes force is approximately
3960
![]() m
m![]() s
s![]() , which is a very large negative force. When a particle is accelerated with an initial velocity of 20m
, which is a very large negative force. When a particle is accelerated with an initial velocity of 20m![]() s,
it will instantaneously experience a negative acceleration of 79.2
s,
it will instantaneously experience a negative acceleration of 79.2![]() 10
10![]() m
m![]() s
s![]() . This means that it is not possible for the droplet to travel the
required distance when starting with the stated initial velocity. In fact, the initial velocity must follow
. This means that it is not possible for the droplet to travel the
required distance when starting with the stated initial velocity. In fact, the initial velocity must follow
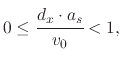 |
(205) |
| (206) |
It may be noted that after leaving the atomizer, the droplets do not travel in the same manner together as they would individually. The interaction between droplets for the ESD system was ignored since, in literature [171], [228], it was suggested that they do not affect the droplet motion significantly. In the ESD system, the electric field is the main factor to the droplet's movement. However, for the pressure system described here, it appears that interaction between droplets plays a larger role. Droplets move through air as a flux and calculating individual droplet's movements in order to find their final location on the wafer surface does not produce a match to the experimental results, shown in Figure 6.19a from [156].
|
There are also several factors which influence
the final thickness of the deposited film. Those include the spraying time, volume of the sprayed solution, air pressure, distance of the atomizer from the
substrate, temperature of the pyrolysis reaction, and time of the solution (SnCl![]() ) aging. It was found in [107] that thicknesses of
the deposited SnO
) aging. It was found in [107] that thicknesses of
the deposited SnO![]() film decrease, when the time interval between its preparation and its use in the pyrolysis reaction increases. A suggestion is made
to use either a freshly made solution or a completely aged solution during spray pyrolysis. During the presented topography simulations, it is assumed
that the nozzle distance to the substrate, air pressure, and solution aging remains constant, while the spray is constantly applied. The nozzle's distance
to the substrate is set to 20cm laterally and 10cm vertically, the air pressure to 1atm, and the solution is freshly prepared. In correspondence, the time and
temperature dependences are investigated in the model.
film decrease, when the time interval between its preparation and its use in the pyrolysis reaction increases. A suggestion is made
to use either a freshly made solution or a completely aged solution during spray pyrolysis. During the presented topography simulations, it is assumed
that the nozzle distance to the substrate, air pressure, and solution aging remains constant, while the spray is constantly applied. The nozzle's distance
to the substrate is set to 20cm laterally and 10cm vertically, the air pressure to 1atm, and the solution is freshly prepared. In correspondence, the time and
temperature dependences are investigated in the model.
Experimental data [156], [211] suggest a linear dependence on spray time and a logarithmic dependence on wafer temperature
for the growth rate of the deposited SnO![]() layer. A good agreement is given by the Arrhenius expression
layer. A good agreement is given by the Arrhenius expression
| (207) |