6.4.3.1 Cospherical Point Sets

Under exact arithmetics degenerate cases result in a compound of points $P_{c,i}$ with identical $\lambda_{c}$. The fourth vertex cannot anymore be determined by minimizing $\lambda$ (Crit. 6.2). Given a set of points $P_{c,i}$ with $\lambda_{c}$ the original algorithm results in overlapping tetrahedra and crossed edges. Several two-dimensional situations are depicted in Fig. 6.24. Figure 6.25 shows an error prone situation with a three-dimensional cospherical point set.

Figure 6.24: (a) Overlapping triangles which share two points (b) Only one common point (c) No points are shared (d) The convex local sphere boundary, LSPB

Figure 6.25: Possible error in a three-dimensional tetrahedralization of a cospherical point set.

Figure 6.26: Approximately cospherical points can form unexpected constellations.

Figure 6.27: The advancing front of the global queue does not pass through a subset of cospherical points.

A valid tessellation cuts the domain in such pieces that the union of all pieces yields exactly the domain. Theoretically, minimizing $\lambda$ suffices to produce a valid tessellation if no such point sets $P_{c,i}$ exist. Practically, this is not even the case for a unique Delaunay Triangulation due to finite precision arithmetics. The strict adherence to the $\lambda$ criterion may force the generation of overlapping elements due to numerical errors [176]. The problem of finite precision arithmetics and of degenerate point sets are closely related.

If one wants to avoid the costly implementation of adaptive precision algorithms and floating point filters [161,48,54,11], one cannot rely on a solution for exactly cospherical points $P_{c,i}$, but has to detect and treat approximately cospherical points $\tilde{P}_{c,i}$ with corresponding $\lambda_{c,i}$ from an algorithmic point of view.

At first must be a robust detection of $\tilde{P}_{c,i}$ which is a crucial task and cannot be achieved by a simple epsilon region where $\lambda_{c,i} \in [\lambda_{\min}, \lambda_{\min} + \varepsilon]$. Inconsistencies due to points that lie close to the border of the epsilon region would be inherent. Numerically they might appear at one time inside of the epsilon region and at another time outside of it. Therefore, an adaptive epsilon region has been implemented which involves a sorting algorithm.

$$\begin{eqnarray*} \lambda_{c,i} & \in & \{\lambda_{1}, \lambda_{2}, \ldots, \lam... ...on \ \ \wedge \\ \lambda_{n+1} - \lambda_{n} & > & \varepsilon \end{eqnarray*}$$

Another critical situation can be observed in Fig. 6.26. The indicated point belongs to an epsilon region, but it somehow cannot be considered to belong to the set of cospherical points. An algorithm to deal with approximately cospherical points $\tilde{P}_{c,i}$ must be prepared for such cases as well.

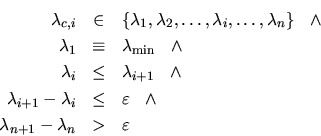
The solution is to treat the points $\tilde{P}_{c,i}$ as an isolated tetrahedralization sub-problem forming a single step in the overall modified advancing front algorithm. Thereby the tetrahedralization technique for the sub-problem is performed by a local instance of the modified advancing front algorithm with a specific alteration described in the following paragraphs. A local instance of the algorithm means that a second queue is built to hold the local advancing front of the tetrahedralization of the sub-problem. An ortho-product point distribution consists of a large number of cospherical point subsets which are regularly stacked. The global advancing front for such an example is shown in Fig. 6.27. One can clearly observe how each subset is treated in a single step from a global point of view.

The local second queue can only provide the frame for the entire solution to the problem of cospherical point sets. Another specific alteration of the tetrahedralization algorithm is required. The enhancement is at first explained for the ideal case of exact cospherical points $P_{c,i}$. The local boundary of the point set is convex (Fig. 6.24-d, convex LSPB). The special tetrahedralization of this sphere is constructed in the following way. Consider a tetrahedralization with a convex boundary. A tetrahedron can be created by linking a point located anywhere outside the tetrahedralization to any triangle of the boundary that has a positive minimum distance to that point. Regardless which triangle of the boundary (with positive minimum distance) is taken the created tetrahedron cannot penetrate the existing tetrahedralization. If this single point is not only linked to one triangle, but to all triangles of the convex boundary that have positive minimum distance to the point, the result is again a tetrahedralization with a convex boundary. The tetrahedralization can be expanded point by point while keeping the temporary boundary convex. The gain from such a method can be immediately seen in Fig. 6.25. If the boundary would have been kept convex during the generation of the in the figure depicted tetrahedron, the error prone situation would have been avoided. The creation of a new tetrahedron could not lead to penetrations.

If the points are located on the perimeter of a sphere, the order in which the points are added to the tetrahedralization will not matter. Any point will be outside of the tetrahedralization of the other points. Also, any tetrahedralization of such points will be a Delaunay Triangulation. Thus, the convex LSPB can be tetrahedralized in this way with a slightly altered advancing front algorithm.

Starting with a base triangle a fourth point from the set of cospherical points is chosen to generate a tetrahedron. The first tetrahedron of the sphere forms a temporary convex boundary to which the other points of the sphere are added one after another. The temporary boundary is kept convex by ``looking back'' from each fourth point of the last generated tetrahedron to link it to all triangles with a positive minimum distance and thereby creating several tetrahedra in one step.

Once the LSPB is completely tetrahedralized, the ``looking back'' algorithm becomes unnecessary and it is returned to the normal tetrahedra growth process. Note that ``looking back'' and checking the minimum distance to the triangles is only required for triangles which belong to the tetrahedralization of the LSPB. As expected the implementation uses a temporary second higher priority queue for the advancing front within the sphere. Once the set $P_{c,i}$ is encountered and processed no later penetrations are possible.

The algorithm is generalized to tetrahedralize the points $\tilde{P}_{c,i}$ which possess general locations not exactly on the perimeter of a sphere. They do not necessarily form a convex Delaunay boundary. The $\lambda$ criterion (Crit. 6.2) is applied for each generated tetrahedron. The point location must take all points in the search region into account (not only points from the subset $\tilde{P}_{c,i}$). If the criterion cannot be satisfied by a point of the subset $\tilde{P}_{c,i}$ with a small tolerance $\varepsilon$, the tetrahedron will not be created. The temporary boundary to which the points $\tilde{P}_{c,i}$ are added thus can contain non-convex regions which will be specially marked. If a point is being linked to all triangles with positive minimum distance such marked triangles are excluded.