



Next: 5.7 Delaunay Slivers
Up: 5. Delaunay Triangulation
Previous: 5.5.2 Conforming Delaunay Triangulation
5.6 Steiner Points and Steiner Triangulation
In the context of a Delaunay Triangulation and other optimal
triangulations/tetrahedralizations Steiner points refer to
points which are added to the set of vertices of the input
PSLG/PLC 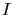 .
The name does not indicate a specific location for the added point.
While refinement is quite naturally considered for mesh generation
purposes, the addition of Steiner points to a Delaunay Triangulation is a
powerful concept in computational geometry which allows quite
theoretical investigations. It forms the basis for many provable optimal
triangulation algorithms for various quality criteria
[16,15,134].
.
The name does not indicate a specific location for the added point.
While refinement is quite naturally considered for mesh generation
purposes, the addition of Steiner points to a Delaunay Triangulation is a
powerful concept in computational geometry which allows quite
theoretical investigations. It forms the basis for many provable optimal
triangulation algorithms for various quality criteria
[16,15,134].
Figure 5.6:
Steiner point insertion at the circumcenter, removal of
non-Delaunay elements, and triangulation of the resulting cavity.
|
|
One of the most important techniques is the insertion of a Steiner point at
the circumcenter of a badly shaped element. The element is not
necessarily refined itself, because its circumcenter might be located in an
adjacent element. In a subsequent step the Delaunay property is restored
which ensures the destruction of the undesired element because its
circumsphere is not empty. The minimum distance between two points cannot
be reduced unproportionally. The circumsphere of a Delaunay element
contains no other points, hence the inserted circumcenter cannot lie
arbitrarily close to another point. This allows a proof of good grading.
The refinement can be bounded by disallowing the insertion of circumcenters
for circumspheres smaller than a given limit. Then, the insertion process
must terminate, because it runs out of space.
Figure 5.7:
Delaunay Triangulation vs. quality improved Steiner
Triangulation. The original 130 triangles (94 points) were
refined with 128 Steiner points resulting in 376 triangles.
|
|
For example in two dimensions a scheme can be devised to guarantee angles
between 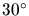 and
and 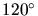 as long as the length of the
boundary edges is within a specified range [28].
Figure 5.6 shows an obtuse triangle which is removed by
inserting its circumcenter and restoration of the Delaunay property.
An example triangulation is shown in Fig. 5.7.
The key idea is that a Steiner point at the circumcenter directly affects
the shortest edge to circumradius ratio quality measure
as long as the length of the
boundary edges is within a specified range [28].
Figure 5.6 shows an obtuse triangle which is removed by
inserting its circumcenter and restoration of the Delaunay property.
An example triangulation is shown in Fig. 5.7.
The key idea is that a Steiner point at the circumcenter directly affects
the shortest edge to circumradius ratio quality measure  (3.1).
(3.1).
Figure 5.8:
The worst case element with a 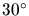 angle and minimum
edge length
angle and minimum
edge length 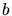 . The largest circumcircle has radius
. The largest circumcircle has radius 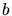 .
.
|
|
To see this it is assumed without loss of generality that
the minimum distance between two points of the input 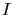 is
is 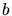 . Steiner
points are inserted as long as elements exist with circumradius greater
than
. Steiner
points are inserted as long as elements exist with circumradius greater
than 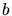 . The restoration of the Delaunay property after each point
insertion is possible with flip operations. Hence, it can be guaranteed due
to the Delaunay property that the inserted points are also not closer than
. The restoration of the Delaunay property after each point
insertion is possible with flip operations. Hence, it can be guaranteed due
to the Delaunay property that the inserted points are also not closer than
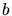 to any other point. Simultaneously it is guaranteed that no circumradius
is greater than
to any other point. Simultaneously it is guaranteed that no circumradius
is greater than 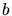 . Termination is guaranteed because each point defines a
disk with radius equal to the minimum distance
. Termination is guaranteed because each point defines a
disk with radius equal to the minimum distance 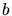 in which no other points
may be located. All such disks sooner or later cover the entire available
space and no more points can be inserted. The resulting edge length ranges
between the minimum distance
in which no other points
may be located. All such disks sooner or later cover the entire available
space and no more points can be inserted. The resulting edge length ranges
between the minimum distance 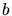 and the maximum
and the maximum 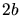 which is possible for
the maximum circumcircle with radius
which is possible for
the maximum circumcircle with radius 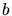 . Hence, the worst (minimal)
quality is
. Hence, the worst (minimal)
quality is
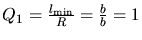 (Fig. 5.8). Because of (3.7) the
minimum angle is
(Fig. 5.8). Because of (3.7) the
minimum angle is
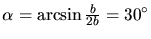 .
.
Figure 5.9:
A naive approach where the bisection of boundary edges and the
insertion of circumcenters runs into an endless loop. The small angle
which causes the insertion of a Steiner point at the center of the
dotted circumcircle is shaded. A better solution can be obtained and
is shown in the bottom left corner.
|
|
An analysis which includes the boundary is more complex
[135,29].
Certain restrictions have to be applied to the edges and facets of  .
As already mentioned the edge lengths must be within a certain range or the
edges must form angles of e.g. no less than
.
As already mentioned the edge lengths must be within a certain range or the
edges must form angles of e.g. no less than 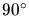 . Naturally, edges
of the input
. Naturally, edges
of the input  can form a sharp angle which is forced into the
triangulation and which cannot be resolved.
If a Steiner point lies outside of the domain defined by
can form a sharp angle which is forced into the
triangulation and which cannot be resolved.
If a Steiner point lies outside of the domain defined by 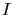 , it
cannot be inserted. Figure 5.9 shows an obtuse element of
which the longest edge is a boundary edge and the circumcenter is outside.
An intuitive approach to bisect the longest edge to destroy the obtuse
angle combined with a minimum angle criterion enforced through Steiner
point insertion at circumcenters may run into an endless loop
(Fig. 5.9). Alternately the boundary edge is further
bisected and a Steiner point added at the circumcenter of the new
element. The boundary edge can never be flipped and the angle never improves.
A solution is to check whether or not a Steiner point
candidate inflicts the smallest sphere criterion of a boundary edge.
As can be seen in Fig. 5.9 the inserted circumcenters
are always located inside of the smallest circle passing through the two
vertices of the boundary edge. In such cases the Steiner point candidate
should be discarded and the boundary edge should be instead refined itself.
Generally, a Steiner point insertion algorithm must stop the attempt to
resolve bad angles in impossible situations due to special
constellations of the edges and facets of
, it
cannot be inserted. Figure 5.9 shows an obtuse element of
which the longest edge is a boundary edge and the circumcenter is outside.
An intuitive approach to bisect the longest edge to destroy the obtuse
angle combined with a minimum angle criterion enforced through Steiner
point insertion at circumcenters may run into an endless loop
(Fig. 5.9). Alternately the boundary edge is further
bisected and a Steiner point added at the circumcenter of the new
element. The boundary edge can never be flipped and the angle never improves.
A solution is to check whether or not a Steiner point
candidate inflicts the smallest sphere criterion of a boundary edge.
As can be seen in Fig. 5.9 the inserted circumcenters
are always located inside of the smallest circle passing through the two
vertices of the boundary edge. In such cases the Steiner point candidate
should be discarded and the boundary edge should be instead refined itself.
Generally, a Steiner point insertion algorithm must stop the attempt to
resolve bad angles in impossible situations due to special
constellations of the edges and facets of 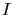 , rather then to cause
excessive refinement. Restrictions on
, rather then to cause
excessive refinement. Restrictions on 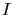 are not acceptable for practical
implementations.
are not acceptable for practical
implementations.
A detailed comparison of Steiner Triangulation algorithms is given in
[162]. Depending on how the boundary is handled different
angle bounds can be achieved [135,28,29].
Often it is experienced that a theoretical minimum angle bound of e.g. 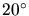 can be increased in practice up to
can be increased in practice up to 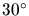 .
A Steiner Triangulation with circumcenters is just as powerful in three
dimensions to improve the shortest edge to circumradius quality criterion
.
A Steiner Triangulation with circumcenters is just as powerful in three
dimensions to improve the shortest edge to circumradius quality criterion
 [30,37]. However, as was pointed out in
Section 3.1 sliver elements are not captured by
[30,37]. However, as was pointed out in
Section 3.1 sliver elements are not captured by  and
are not removed by inserting circumcenters as Steiner points.
A three-dimensional method which promises to avoid all badly shaped
elements and which is based on a two-dimensional approach with Steiner
points [16] is proposed in [109].
and
are not removed by inserting circumcenters as Steiner points.
A three-dimensional method which promises to avoid all badly shaped
elements and which is based on a two-dimensional approach with Steiner
points [16] is proposed in [109].




Next: 5.7 Delaunay Slivers
Up: 5. Delaunay Triangulation
Previous: 5.5.2 Conforming Delaunay Triangulation
Peter Fleischmann
2000-01-20
![]() .
The name does not indicate a specific location for the added point.
While refinement is quite naturally considered for mesh generation
purposes, the addition of Steiner points to a Delaunay Triangulation is a
powerful concept in computational geometry which allows quite
theoretical investigations. It forms the basis for many provable optimal
triangulation algorithms for various quality criteria
[16,15,134].
.
The name does not indicate a specific location for the added point.
While refinement is quite naturally considered for mesh generation
purposes, the addition of Steiner points to a Delaunay Triangulation is a
powerful concept in computational geometry which allows quite
theoretical investigations. It forms the basis for many provable optimal
triangulation algorithms for various quality criteria
[16,15,134].
![\includegraphics [width=0.7\textwidth]{ppl/steinregr.ps}](img243.gif)
![\includegraphics [width=0.7\textwidth]{ppl/area.eps}](img244.gif)
![\includegraphics [height=4.3cm]{ppl/steinerproof.ps}](img246.gif)
![\includegraphics [width=0.95\textwidth]{ppl/steinerproblem.ps}](img250.gif)
![]() can be increased in practice up to
can be increased in practice up to ![]() .
A Steiner Triangulation with circumcenters is just as powerful in three
dimensions to improve the shortest edge to circumradius quality criterion
.
A Steiner Triangulation with circumcenters is just as powerful in three
dimensions to improve the shortest edge to circumradius quality criterion
![]() [30,37]. However, as was pointed out in
Section 3.1 sliver elements are not captured by
[30,37]. However, as was pointed out in
Section 3.1 sliver elements are not captured by ![]() and
are not removed by inserting circumcenters as Steiner points.
A three-dimensional method which promises to avoid all badly shaped
elements and which is based on a two-dimensional approach with Steiner
points [16] is proposed in [109].
and
are not removed by inserting circumcenters as Steiner points.
A three-dimensional method which promises to avoid all badly shaped
elements and which is based on a two-dimensional approach with Steiner
points [16] is proposed in [109].