



Next: 6. Architecture and Implementation
Up: 5. Delaunay Triangulation
Previous: 5.6 Steiner Points and
5.7 Delaunay Slivers
A sliver has been introduced in Section 3.1 as an
element with a very specific bad shape in the context of mesh
generation. They are sometimes also called flat tetrahedra.
Here, in the context of a Delaunay Triangulation and for the following
chapter it is worthwhile to distinguish three sliver versions
(Fig. 5.10).
- A sliver tetrahedron which does not satisfy the Delaunay criterion.
- A sliver tetrahedron which satisfies the Delaunay criterion in a
strict sense. Its vertices are not part of a set of cospherical points and
the Delaunay Triangulation around the sliver is unique.
- A sliver tetrahedron which satisfies the Delaunay criterion, but which
is composed of vertices out of a set of cospherical points. The Delaunay
Triangulation is not unique.
Figure 5.10:
(a) Non-Delaunay sliver with circumsphere and two adjacent
tetrahedra in the back (b) Strict sense Delaunay sliver with an empty
circumsphere (c) Delaunay sliver with a cospherical point set.
|
|
The first type is of less importance and will clearly be absent in a
Delaunay Triangulation.
The second type, a Delaunay sliver, unfortunately exists in
a Delaunay Triangulation for a given point set 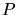 in three dimensions.
The various optimality properties of a Delaunay Triangulation were given in
Section 5.1. The minimum dihedral angle is not guaranteed to
be optimal in three dimensions. A different non-Delaunay tetrahedralization
might exist which avoids slivers with small dihedral angles but which
is in other sense less optimal.
In theory manipulation of
in three dimensions.
The various optimality properties of a Delaunay Triangulation were given in
Section 5.1. The minimum dihedral angle is not guaranteed to
be optimal in three dimensions. A different non-Delaunay tetrahedralization
might exist which avoids slivers with small dihedral angles but which
is in other sense less optimal.
In theory manipulation of 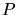 by constructing a Steiner Triangulation with
Steiner points at circumcenters does not help to eliminate Delaunay slivers.
The question arises whether a different type of Steiner point insertion is
capable to manipulate
by constructing a Steiner Triangulation with
Steiner points at circumcenters does not help to eliminate Delaunay slivers.
The question arises whether a different type of Steiner point insertion is
capable to manipulate 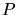 such that a Delaunay Triangulation results which
does not contain Delaunay slivers. Alternatively, it would be of interest
to examine how pronounced the occurrence of Delaunay slivers is in a
practical mesh and how often they really survive the insertion of Steiner
points at circumcenters in practice. Also, there is a chance that the
third type sliver which is less critical exists much more often than a
strict sense Delaunay sliver. Local transformations can be applied while
maintaining the Delaunay property. The Delaunay Triangulation is not
unique. The mesh examples in Section 3.2.3 have shown two
different Delaunay Triangulations of an identical ortho-product point set
where only one tetrahedralization contained sliver elements.
A similar distinction of types can be made for the twisted prism. Its
relation to slivers will be important in the next chapter
(Section 6.4.3, Fig. 6.29).
such that a Delaunay Triangulation results which
does not contain Delaunay slivers. Alternatively, it would be of interest
to examine how pronounced the occurrence of Delaunay slivers is in a
practical mesh and how often they really survive the insertion of Steiner
points at circumcenters in practice. Also, there is a chance that the
third type sliver which is less critical exists much more often than a
strict sense Delaunay sliver. Local transformations can be applied while
maintaining the Delaunay property. The Delaunay Triangulation is not
unique. The mesh examples in Section 3.2.3 have shown two
different Delaunay Triangulations of an identical ortho-product point set
where only one tetrahedralization contained sliver elements.
A similar distinction of types can be made for the twisted prism. Its
relation to slivers will be important in the next chapter
(Section 6.4.3, Fig. 6.29).




Next: 6. Architecture and Implementation
Up: 5. Delaunay Triangulation
Previous: 5.6 Steiner Points and
Peter Fleischmann
2000-01-20
![\includegraphics [width=0.9\textwidth]{ppl/slivertypes.ps}](img252.gif)
![\includegraphics [width=0.9\textwidth]{ppl/slivertypes.ps}](img252.gif)