



Next: 6.4.2 Point Location
Up: 6.4 Volume Tetrahedralization
Previous: 6.4 Volume Tetrahedralization
Figure 6.15 shows the flow diagram of the modified advancing
front algorithm. Delaunay triangles are extracted from the surface
triangulation to form an oriented initial front.
These triangles have the purpose of a seed which is inserted into a queue
to ``grow'' tetrahedra.
Figure 6.15:
Modified advancing front algorithm.
|
|
The algorithm starts with a non-empty queue. It does not require the queue
to hold all surface triangles which represent the boundary. One triangle
per enclosed segment is sufficient. The surface triangulation has two
purposes.
- It provides the initial front for the advancing front algorithm to
start with. One triangle per segment is enough and is called a seed
triangle.
- It provides a border for the advancing front algorithm which cannot
be passed.
The triangles of the initial front and all later generated triangles of the
advancing front have an orientation defined by the order of their vertices.
Given a seed triangle (which is taken from the queue) a tetrahedron is
attached to that side of the triangle which faces the half space in which
its normal vector is directed. The tetrahedron is constructed with a
a fourth point which has a positive distance to the seed triangle relative
to its normal vector.
In this way a front side and a back side of triangles is
distinguished.
Figure 6.16:
The triangle to which the next tetrahedron is attached is
shaded for each step.
|
|
Repeatedly attaching tetrahedra to the front sides of the triangles of
the queue, removing them from the queue when they have been processed,
and inserting new triangles into the queue leads to a growth process of
tetrahedra (Fig. 6.16, Fig. 6.17).
Hence, the queued triangles form the advancing front at all times.
It advances when a new tetrahedron (attached to a triangle which is removed
from the queue) generates new triangles which are inserted into the queue.
Generally, a created tetrahedron can produce any number between 0 and
3 new triangles. During the beginning of the tetrahedralization process
each created tetrahedron will more likely produce 3 new triangles and the
size of the queue will increase rapidly.
Later on the advancing front will merge with itself or parts of the
surface triangulation and fewer new triangles are produced.
A tetrahedron consists of 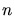 new triangles,
new triangles, 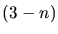 previously generated
triangles, and the triangle to which it is attached. The
previously generated
triangles, and the triangle to which it is attached. The 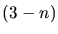 previously generated triangles must have been previously inserted into
the queue or belong to the initial surface triangulation.
They are part of the advancing front. When they are encountered during the
creation of a new tetrahedron, they are removed from the queue and the
advancing front is stopped. If
previously generated triangles must have been previously inserted into
the queue or belong to the initial surface triangulation.
They are part of the advancing front. When they are encountered during the
creation of a new tetrahedron, they are removed from the queue and the
advancing front is stopped. If 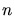 is zero the creation of the tetrahedron
results in a decrease of the size of the queue.
When the queue has run empty the meshing process terminates.
is zero the creation of the tetrahedron
results in a decrease of the size of the queue.
When the queue has run empty the meshing process terminates.
Figure 6.17:
A snapshot of the growing mesh generated by the modified
advancing front algorithm.
|
|
The following questions arise:
- What degree of freedom does the algorithm have to choose a
tetrahedron to be attached to a triangle of the queue ? What kind of
tetrahedron will be chosen ?
- How is it guaranteed that the advancing front does not pass
through itself or the given boundary triangulation ?
- How is it guaranteed that no part of the domain remains
untetrahedralized ?
First it is assumed that the Delaunay Triangulation is unique and
degenerate point sets do not exist.
Given a fixed mesh point distribution and an oriented triangle only one
point can complement the triangle to form a valid Delaunay tetrahedron to
be attached to the triangle's front side. The meshing algorithm will choose
to create exactly this tetrahedron. Intrinsically it is not able to create
non-Delaunay tetrahedra as will be seen later on.
To answer the second question the following is observed.
Lemma 6.1
The advancing front cannot build loops, intersect or
overlap with itself, or pass through Delaunay borders as long as it is
guaranteed that identical triangles are never stored more than once.
Proof 6.1
Under the assumption of a unique Delaunay Triangulation any Delaunay
triangle must be present within the tetrahedralization. No Delaunay
triangle exists which is not part of the tetrahedralization. If one or
more such triangles would exist the Delaunay Triangulation would not be
unique. Given the facts that the algorithm only produces Delaunay
tetrahedra and the advancing front separates the tetrahedralized domain
from the untetrahedralized domain, it follows that at all times the
advancing front consists entirely of Delaunay triangles. Assume that one
part of the advancing front passes through another part of the advancing
front. Then, part of the front must be located in the interior of a
tetrahedralized region. Since the front consists of Delaunay triangles
they must be part of the unique tetrahedralization. Hence, during the
tetrahedralization Delaunay triangles must have been produced and stored
where identical copies already existed as part of the front.
Such a test whether or not an identical triangle already exists is trivial
and does not cost performance. It guarantees that the algorithm terminates.
Since no Delaunay triangles are generated more than once and the overall
number of Delaunay triangles 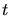 in a Delaunay Triangulation is finite, the
algorithm terminates after at most
in a Delaunay Triangulation is finite, the
algorithm terminates after at most 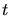 steps.
steps.
To see that complex structures are rigorously meshed regardless of whether
or not they are multiple connected the following is examined.
Lemma 6.2
No volume is left untetrahedralized unless it is enclosed by a surface
triangulation to which no seed was provided.
Proof 6.2
Assume that part of the domain remains untetrahedralized and the
algorithm has terminated. The algorithm must only terminate if the queue
holding the advancing front is empty.
The untetrahedralized region must be separated from the tetrahedralized
region or the outside of the domain by a surface triangulation 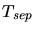 .
First, assume that
.
First, assume that 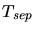 contains at least one triangle that is part
of a tetrahedron and was generated during the tetrahedralization
process. Then, this triangle must have been inserted into the
queue. It can be attached to at most one tetrahedron, because
contains at least one triangle that is part
of a tetrahedron and was generated during the tetrahedralization
process. Then, this triangle must have been inserted into the
queue. It can be attached to at most one tetrahedron, because
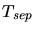 was defined to be the border between the tetrahedralized
and the untetrahedralized region.
Since it would have only been removed from the queue if a second
tetrahedron would have been attached to it, the queue cannot be empty and
the algorithm cannot have terminated. Second, assume that
was defined to be the border between the tetrahedralized
and the untetrahedralized region.
Since it would have only been removed from the queue if a second
tetrahedron would have been attached to it, the queue cannot be empty and
the algorithm cannot have terminated. Second, assume that 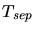 does not contain triangles produced during the tetrahedralization.
Then, it must entirely consist of triangles present in the given boundary
surface triangulation. Since it is a closed region, the boundary defines
a segment. Under the requirement that at least one boundary triangle per
segment is inserted into the queue the algorithm cannot have
terminated.
does not contain triangles produced during the tetrahedralization.
Then, it must entirely consist of triangles present in the given boundary
surface triangulation. Since it is a closed region, the boundary defines
a segment. Under the requirement that at least one boundary triangle per
segment is inserted into the queue the algorithm cannot have
terminated.




Next: 6.4.2 Point Location
Up: 6.4 Volume Tetrahedralization
Previous: 6.4 Volume Tetrahedralization
Peter Fleischmann
2000-01-20
![\includegraphics [height=12cm]{ppl/flow_alg2.ps}](img299.gif)
![]() in a Delaunay Triangulation is finite, the
algorithm terminates after at most
in a Delaunay Triangulation is finite, the
algorithm terminates after at most ![]() steps.
steps.