6.4.2 Point Location

Figure 6.18: A non-uniform point bucketing scheme and a rectangular search region which is aligned with the bounding box and which is associated with a circle and a given $\lambda$ value (two-dimensional analogy).

An efficient data structure for point bucketing is crucial to quickly locate the fourth vertex among all mesh points which completes a triangle from the queue to form a Delaunay tetrahedron. The currently processed triangle which was taken from the queue is called a base triangle. The advancing front holds Delaunay triangles, hence any base triangle satisfies the Delaunay criterion. A local region around the base triangle needs to be searched for to find the correct fourth point. The border of this region is defined by a sphere containing the circumcircle of the base triangle. The radius of the sphere will be increased as long as the sphere does not contain other points. A sketch for the two-dimensional case is depicted in Fig. 6.18 where an edge corresponds to the base triangle. It is evident that one sphere must exist which does not hold any other points due to the Delaunay property of the base triangle. In fact, the way the region around the base triangle is examined resembles closely the Delaunay sphere criterion. The size of the sphere is increased so that exactly one other point (than the three points of the base triangle) is located on the perimeter of the sphere. This point is the seeked fourth vertex of the tetrahedron. It is evident that the tetrahedron must satisfy the Delaunay criterion, because its circumsphere does not contain any other point. For one base triangle two spheres exist that correspond to a tetrahedron on each side. The algorithm will only attach a tetrahedron to the front side of the base triangle as previously explained. It will therefore increase the size of the sphere into the direction of the normal vector of the base triangle. This is expressed by a signed increase of the normal distance $\lambda$ between the center $M$ of the sphere and the base triangle. The normal distance can be positive or negative. The point $H$ denotes the circumcenter of the base triangle and $\vec{n}$ its unit length normal vector. The smallest sphere is characterized by $\lambda = 0$. A negative $\lambda$ denotes a sphere which covers a larger area on the back side than on the front side of the triangle.

$$\lambda := \vec{HM} \cdot \vec{n}$$

The spherical search region fits into a cubic search region which can always be aligned with the bounding box (Fig. 6.18). This allows for an efficient non-uniform point bucketing scheme to locate points within the search region. All points are stored and maintained at all times in a point bucket octree [142]. Any rectangular area aligned with the bounding box can be searched by traversing the tree data structure.

Figure 6.19: Every found point $P_{i}$ in the search region defines a $\lambda _{i}$.

The gradual increase of the size of the search region does not cost much performance. If the sphere is too small no points will be located inside the search region and the effort of traversing the octree is minimal. The case when exactly one point (the fourth vertex of the tetrahedron) is found, is ideal. Usually, the search region will contain several points. In such a case the size of the sphere defining the search region will not be reduced until only a single point is contained. Instead $\lambda _{i}$ is computed from $M_{i}$ which is the center of the sphere defined by the point $P_{i}$ and the base triangle (Fig. 6.19). $\vec{X}$ is the location vector of one of the three vertices of the base triangle.

$$\lambda_{i} = (\vec{M}_{i}-\vec{X}) \cdot \vec{n}$$

From the collection of points $P_{i}$ the correct fourth point can be chosen by minimizing $\lambda _{i}$.

Criterion 6.2 (Minimum $\lambda$)   Let $P_{i}$ with corresponding $\lambda _{i}$ be a complete set of all points which are located in a spherical search region in $R^{3}$ defined by a Delaunay triangle $t$ and a value $\lambda_{\max} \geq \lambda_{i}$. The point $P_{j}$ and the Delaunay triangle $t$ form a Delaunay tetrahedron, if and only if $\lambda_{j} = \lambda_{\min}$.

Figure 6.20: The scope of $\lambda$ for the two-dimensional case. Depending on the location of a point its $\lambda$ value can reach a critical value. Singular regions of $\lambda$ are indicated.

The scope of the possible $\lambda$ values is numerically a delicate matter. The robust implementation applies an additional insphere test. Figure 6.20 shows the two-dimensional analogy. The normal distance of a point $P$ to the plane containing the base triangle (in two dimensions an edge) is $d$. The point $P_{1}$ has $d=0$ and the point $P_{2}$ has a positive $d$. The algorithm has to determine which of the two points $P_{1}$ and $P_{2}$ is the correct point. The correct triangle in the two-dimensional case is drawn with dashed lines. The various possible locations of a point are denoted with the corresponding $\lambda$ values. The location of points with $\lambda = 0$ is shown by the dashed circle. The point $P_{1}$ is on a numerical critical location:

$$\begin{eqnarray*} \lim_{d \rightarrow 0^{+}} \lambda_{P_{1}} & = & +\infty \\ \lim_{d \rightarrow 0^{-}} \lambda_{P_{1}} & = & -\infty \end{eqnarray*}$$

Figure 6.21: An open surface description and the growing mesh.

Figure 6.22: Complete boundary representation after tetrahedralization.

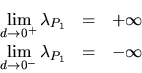
A more flexible algorithm allows boundaries which do not form a closed surface. This generalization is implemented as follows. If no fourth vertex can be found after gradually increasing the search region up to the size of the bounding box, the base triangle will be converted and stored as a boundary triangle. In this way new boundary triangles can be generated during the tetrahedralization process at locally convex regions of the mesh point distribution. Figure 6.21 shows an example of an open surface description and a snapshot of the meshing process. Figure 6.22 depicts the complete boundary including the generated boundary triangles after tetrahedralization.

The octree search and the $\lambda$ criterion introduce the logarithm into the overall time complexity $O(n\log n)$ where $n$ is the number of tetrahedra. For randomized point distributions the number of tetrahedra grows approximately linear with the number of points (Fig. 6.23). The algorithm runs in optimal time. The performance is given in Tab. 6.1.

Figure 6.23: Runtime on an HP 9000-735/100Mhz

Table 6.1: Runtime on an HP 9000-735/100Mhz

quantity of ...			CPU time
points	tetrahedra	triangles	(in sec)
103	535	1098	0.2
503	3016	6112	1.4
703	4323	8739	2.1
1003	6268	12635	3.3
1503	9494	19107	5.1
2003	12713	25557	6.8
2503	16076	32300	8.8
3003	19394	38967	11.1
4003	25969	52140	15.6
5003	32691	65605	19.7
10003	65927	132160	46.5
20003	132854	266133	92.0
30003	199613	399756	145.0
40003	266899	534405	207.0