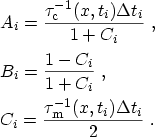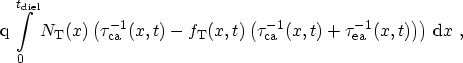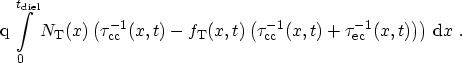3.8.2.4 Transient Current
Models of trap-assisted transitions are commonly employed to calculate
steady-state SILC in MOS capacitors, while transient SILC has hardly been
studied [194,205]. However, transient tunneling current
becomes important at high switching speed where the transients of the trap
charging and discharging processes may degrade signal integrity. For the
calculation of transient SILC it is necessary to calculate capture and
emission times at each time step. Considering a spatial trap distribution
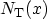 across the dielectric layer, the rate equation for the concentration
of occupied traps at position
across the dielectric layer, the rate equation for the concentration
of occupied traps at position  reads
reads
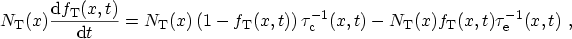 |
(3.150) |
where
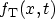 is the trap occupancy function and
is the trap occupancy function and
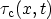 and
and
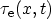 are the inverse capture and emission times of electrons by a trap
placed at position
are the inverse capture and emission times of electrons by a trap
placed at position  . In the static case capture and emission processes are
in equilibrium and
. In the static case capture and emission processes are
in equilibrium and
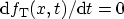 . In the transient case,
however, capture and emission times include transitions from the cathode and
the anode (compare Section 3.8.1.2 and Fig. 3.16)
. In the transient case,
however, capture and emission times include transitions from the cathode and
the anode (compare Section 3.8.1.2 and Fig. 3.16)
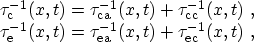 |
(3.151) |
where
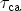 and
and
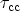 are the capture times to the anode and to the
cathode, and
are the capture times to the anode and to the
cathode, and
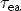 and
and
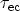 the corresponding emission times. To
calculate the local trap occupancy, the differential equation
(3.150) must be solved. If the capture and emission times
the corresponding emission times. To
calculate the local trap occupancy, the differential equation
(3.150) must be solved. If the capture and emission times
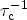 and
and
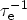 are constant over time, like in a discharging
process with a constant potential distribution, the solution of
(3.150) can be given in a closed form
are constant over time, like in a discharging
process with a constant potential distribution, the solution of
(3.150) can be given in a closed form
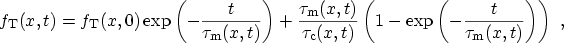 |
(3.152) |
with
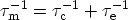 .
.
A more general approach is to look at the change of the trap distribution at
discrete time steps. Integration of (3.150) in time between
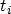 and
and 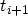 and changing to discrete time steps yields
and changing to discrete time steps yields
where the abbreviations
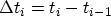 and
and
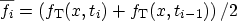 have been used. Thus it is possible to
write the trap distribution over time in the following recursive manner:
have been used. Thus it is possible to
write the trap distribution over time in the following recursive manner:
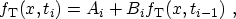 |
(3.153) |
where the symbols 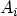 ,
, 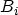 , and
, and 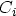 are calculated from
are calculated from
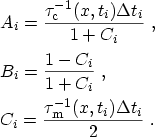 |
(3.154) |
Once the time-dependent occupancy function in the dielectric is known, the
tunnel current through each of the interfaces is
A. Gehring: Simulation of Tunneling in Semiconductor Devices
![]() and
and ![]() and changing to discrete time steps yields
and changing to discrete time steps yields