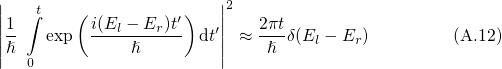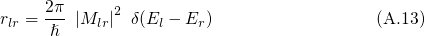
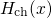 and
and 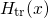 , respectively. This means that the attractive trap potential
, respectively. This means that the attractive trap potential
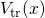 is not accounted for in
is not accounted for in 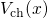 so that
so that 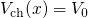 in the trap
region. Vice versa, the channel potential
in the trap
region. Vice versa, the channel potential 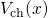 is omitted in
is omitted in 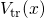 , which
consequently takes the value
, which
consequently takes the value 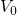 in the channel region.
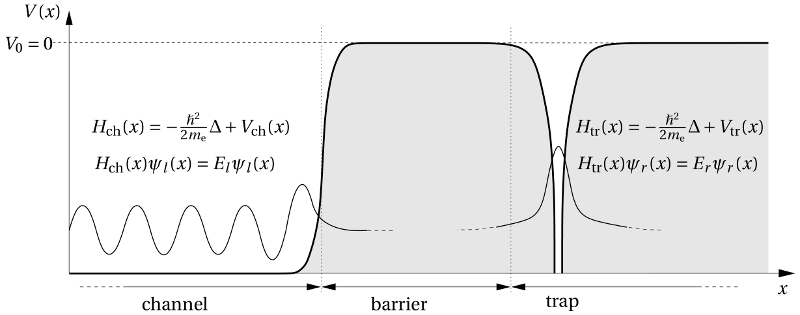
in the channel region.Fermi’s golden rule provides one way to calculate the transition rate between two certain quantum mechanically defined states. Due to its generality, it has various applications in the field of atomic, nuclear, and solid-state physics. In the case of NBTI, it is of most interest for charge transfer reactions and electron tunneling in particular. In the following, Fermi’s golden rule is derived for electron tunneling from the substrate into an oxide defect as illustrated in Fig. A.1.

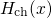 and
and 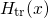 , respectively. This means that the attractive trap potential
, respectively. This means that the attractive trap potential
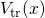 is not accounted for in
is not accounted for in 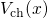 so that
so that 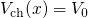 in the trap
region. Vice versa, the channel potential
in the trap
region. Vice versa, the channel potential 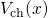 is omitted in
is omitted in 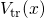 , which
consequently takes the value
, which
consequently takes the value 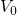 in the channel region.
in the channel region.The system is divided into three separate regions, namely the channel, the insulator
barrier, and the trap region. The electron wavefunctions 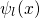 and
and 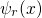 extend
into the classically forbidden barrier region. Their overlap actually leads to a
mutual influence between the channel and the trap system. However, this
influence is assumed to be negligible so that both systems can be treated
independently to first order. This justifies the assumption that in a first
approximation the channel and the trap system can be described by their own
Hamiltonians
extend
into the classically forbidden barrier region. Their overlap actually leads to a
mutual influence between the channel and the trap system. However, this
influence is assumed to be negligible so that both systems can be treated
independently to first order. This justifies the assumption that in a first
approximation the channel and the trap system can be described by their own
Hamiltonians 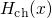 and
and 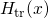 . For the derivation of the tunneling
rate, the Hamiltonian of the common system is taken as a starting point.
. For the derivation of the tunneling
rate, the Hamiltonian of the common system is taken as a starting point.
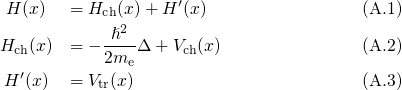
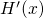 is viewed as the time-dependent perturbation that triggers the scattering
from the band states
is viewed as the time-dependent perturbation that triggers the scattering
from the band states 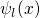 into the trap states
into the trap states 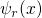 . The solution
. The solution 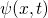 of the
common system
of the
common system 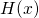 can be written as a linear combination of the eigen
wavefunctions
can be written as a linear combination of the eigen
wavefunctions 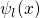 of the unperturbed system
of the unperturbed system 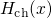 .
.
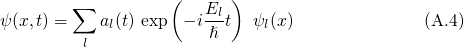
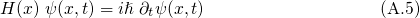
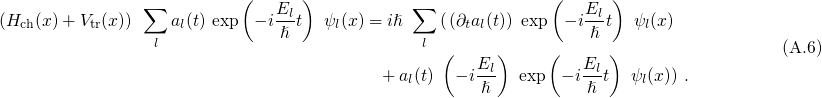
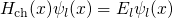 , the above equation simplifies to
, the above equation simplifies to 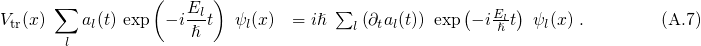
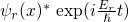 from the left and integrating over space
yields
from the left and integrating over space
yields 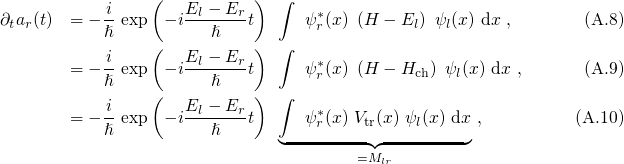
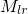 is referred to as the matrix element.
is referred to as the matrix element. 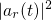 gives the transition
probability
gives the transition
probability 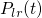 that an electron initially located in the state
that an electron initially located in the state 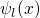 , evolves into
the final states
, evolves into
the final states 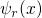 after a time t. Therefore, it must be divided by the time
after a time t. Therefore, it must be divided by the time 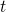 in
order to yield the transition rate
in
order to yield the transition rate 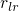 . The integrand is sharply peaked at
. The integrand is sharply peaked at 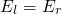 and can be approximated as a
and can be approximated as a
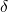 -function.
-function.