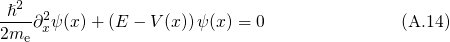
The WKB method [102] is an approximative semiclassical approach to compute the stationary solution of the Schrödinger equation without struggling with the difficulties of a second order differential equation. Taking the time-independent, one-dimensional Schrödinger equation
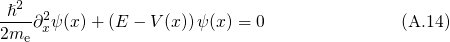

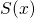 by its expansion in power series of
by its expansion in power series of 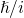
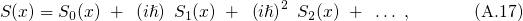
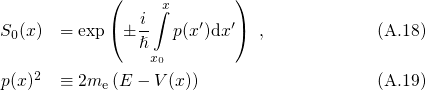
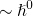 and for terms of the order
and for terms of the order 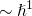 . Integrating (A.20), one obtains
. Integrating (A.20), one obtains 
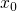 to an arbitrary point
to an arbitrary point 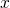 .
. 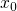 is also referred
to as the classical turning point, where the particle energy
is also referred
to as the classical turning point, where the particle energy 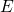 equals the potential
energy
equals the potential
energy 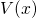 . Note that close to this point, the WKB approximation breaks down
and the expression for the wavefunction diverges since
. Note that close to this point, the WKB approximation breaks down
and the expression for the wavefunction diverges since 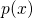 in the denominator
approaches zero. As a result, the wavefunction left and right to this point cannot be
adjusted, which is the case at the discontinuity of the semiconductor-dielectric
interface for instance. One way to overcome this problem is to apply Langer’s
procedure [102], which is not presented here. The above formula also applies to
classical forbidden regions where the particle energy
in the denominator
approaches zero. As a result, the wavefunction left and right to this point cannot be
adjusted, which is the case at the discontinuity of the semiconductor-dielectric
interface for instance. One way to overcome this problem is to apply Langer’s
procedure [102], which is not presented here. The above formula also applies to
classical forbidden regions where the particle energy 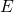 lies below the potential
barrier
lies below the potential
barrier 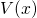 .
.