


Next: 2.3 Constitutive Relation Formulation
Up: 2. Circuit Equations
Previous: 2.1 Nodal Approach
The modified nodal approach (MNA) [31] overcomes the above stated
shortcomings by introducing branch currents as independent variables which are
available to formulate the device constitutive relations. The MNA
enjoyed large popularity due to its simplicity and ease of implementation and
is employed in SPICE which can safely be labeled the standard simulation
program. However, the numerically well behaved circuit matrix obtained by the
NA is distorted by those additional equations, and some additional measures
have to be taken to allow for the use of iterative solvers.
An ideal voltage source introduces a direct relationship between the node voltages
it is connected to of the form
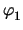 -
- 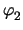 = V0 .
= V0 . |
(2.16) |
The current flowing through this source is added as an additional unknown
and is used to formulated KCL at the respective nodes. Hence, the following
stamp is obtained
| yx, y |
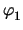 |
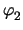 |
I |
r |
| n1 |
|
|
-1 |
|
| n2 |
|
|
1 |
|
| I |
-1 |
1 |
|
V0 |
As pointed out above, these additional equations can produce a zero entry in
the main-diagonal, hence an iterative solver cannot be used directly. Zero
diagonals can be avoided by exchanging the rows of the admittance matrix
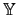 following a simple algorithm [43] which guarantees non-zero
main-diagonal entries. Failure of this algorithm denotes voltage source loops
which indicate an error in the circuit description.
following a simple algorithm [43] which guarantees non-zero
main-diagonal entries. Failure of this algorithm denotes voltage source loops
which indicate an error in the circuit description.
In general, the MNA matrix can be expressed in the form
where
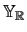 is a reduced form of the nodal matrix excluding the
contributions due to voltage sources, current controlling elements,
etc.,
is a reduced form of the nodal matrix excluding the
contributions due to voltage sources, current controlling elements,
etc.,
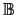 contains partial derivatives of the Kirchhoff current
equations with respect to the additional current variables which are normally
contains partial derivatives of the Kirchhoff current
equations with respect to the additional current variables which are normally
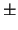 1. The additional branch constitutive relations, derived with respect to the
unknown vector are represented by the matrices
1. The additional branch constitutive relations, derived with respect to the
unknown vector are represented by the matrices
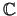 and
and
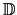 . The
vectors
J and
F are the excitation vectors. From an implementations
point of view it is advantageous to consider the contributions of each circuit
element to the MNA matrix separately.
. The
vectors
J and
F are the excitation vectors. From an implementations
point of view it is advantageous to consider the contributions of each circuit
element to the MNA matrix separately.



Next: 2.3 Constitutive Relation Formulation
Up: 2. Circuit Equations
Previous: 2.1 Nodal Approach
Tibor Grasser
1999-05-31
![$ \underbrace{\left[ \begin{array}{cc} \mathbb{Y_R} & \mathbb{B}\\ \mathbb{C} & \mathbb{D}\\ \end{array} \right]}_{\mathbb{\displaystyle Y}}^{}\,$](img71.gif) .
. ![$ \underbrace{\left[ \begin{array}{c} \boldsymbol{\varphi}\\ \mathbf{I} \end{array} \right]}_{\mathbf{\displaystyle x}}^{}\,$](img72.gif) =
= ![$ \underbrace{\left[ \begin{array}{c} \mathbf{J} \\ \mathbf{F} \end{array} \right]}_{\mathbf{\displaystyle r}}^{}\,$](img73.gif)