2. Circuit Equations

A physical circuit consists of an interconnection of circuit elements. Two different aspects have to be considered when developing a mathematical model for a circuit.

• The circuit equations must satisfy Kirchhoff's topological laws which are
  • Kirchhoff's current law (KCL) which states that the algebraic sum of the currents leaving a circuit node must be zero at every instant of time and
  • Kirchhoff's voltage law (KVL) which states that the algebraic sum of voltages around any loop of the circuit must be zero at every instant of time.
• Each circuit element has to satisfy its branch relation which will be called a constitutive relation in the following. There are
  • current-defined branches where the branch current is defined in terms of circuit and device parameters and
  • voltage-defined branches where the branch voltage is defined in terms of circuit and device parameters.
  Devices with N terminals can be described using N ^. (N - 1)/2 branch relations.

It is not necessary to include all branch currents and voltages into the vector of unknowns x. On the other hand it is possible to also include charges and fluxes into x. The wide choice of possible unknown quantities leads to a wide variety of equation formulations that are available. Furthermore, depending on the choice of x, different phenomena may be described and the complexity of the problem varies drastically. From the vast number of published methods, the following two are the most important:

• The nodal approach only allows for current-defined branches and only the node voltages 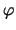$\varphi$ are included into the solution vector x. After obtaining the solution the currents can be calculated from these node voltages. Voltage-defined branches can be introduced without extending the formulation by the use of gyrators [66,70]. To properly account for voltage-defined branches the modified nodal approach has been proposed which allows for introduction of arbitrary branch currents [31].
• Several variants of the tableau approach [6] have been published which can be distinguished by the choice of additional unknowns. This is the most general approach and a wide variety of circuits can be simulated with it. Especially many idealized theoretical circuit elements which cannot be dealt with properly using nodal approaches can be handled using the tableau approach. However, there are several inherent disadvantages with these algorithms. First, they are more complicated to handle than algorithms belonging to the nodal approach family, and secondly they produce ill-conditioned equation systems which are more cumbersome to treat compared to the well-behaved equation systems resulting from the nodal approach.

As the main task of mixed-mode device simulation is to solve realistic devices under dynamic boundary conditions imposed by a circuit, the nodal approach perfectly suits the needs. Hence the following will concentrate on algorithms related to the nodal approach only.