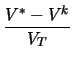


Next: 6.2.5 The New Method
Up: 6.2 Circuit Equation Damping
Previous: 6.2.3 Global Damping Strategy
In conventional circuit simulation it is common practice to limit the contact
voltages before evaluating the compact model. This is illustrated for a simple
diode model represented by the equation
Figure 6.1:
Horizontal and vertical projection of the current solution for a diode.
![\begin{figure}
\begin{center}
\resizebox{7.8cm}{!}{
\psfrag{I}{$\scriptstyle I$}...
...egraphics[width=7.8cm,angle=0]{figures/diode-limit.eps}}\end{center}\end{figure}](img450.gif) |
with IS being the saturation current and
VT = kB . T/q the thermal
voltage. At the Newton iteration step k equation
(6.3) is linearized around the current solution point Vk.
The solution of the linearized system is found as Vk + 1. However,
directly using Vk + 1 (vertical projection) can easily lead to overflow of
the exponential function in (6.3) as shown in
Fig. 6.1. To overcome this problem, horizontal projection
has been introduced. The appropriate expressions are easily derived using
Fig. 6.1. The current change evaluates to
Ik + 1 - Ik =  Vk + 1 - Vk Vk + 1 - Vk . .  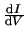
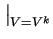 . . |
(6.4) |
Inserting (6.3) gives
exp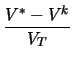 |
= |
1 + 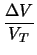 |
(6.5) |
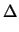 V V |
= |
Vk + 1 - Vk |
(6.6) |
and finally
V* = Vk + VT . ln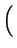 1 + 1 + 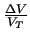
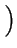 . . |
(6.7) |
However, horizontal projection is only useful for
Vk + 1 > Vcrit.
Below
Vcrit vertical projection obviously delivers better results.
Equation (6.7) can be generalized to arbitrary non-linearities
[32]
V* = Vk + 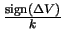 . ln . ln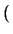 1 + k . | 1 + k . |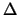 V| V|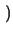 |
(6.8) |
with k being a new scaling factor which can be optimized for each single
device in the course of iteration progress. A larger k gives stronger
damping and hence increases reliability of the algorithm for the price of
longer simulation times. It must be pointed out that this mixed method of
updating is not amenable to an easy description in terms of matrices,
Jacobians, etc., and hence convergence theorems for this method are impossible
to formulate. However, actual experience with this procedure in handling all
types of circuits during the last decades has proven its effectiveness. As
the voltages are damped in an individual manner for each device this damping
algorithm will be termed local in the following. When investigating
(6.3) one notices that
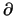 I/
I/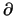 V can become very small for
V
V can become very small for
V  0 which could result in a singular matrix. To prevent this occurrence
a small leakage conductance
Gmin of typically
10-9-
10-12 S is placed in shunt with each junction.
Alternatively
Gmin can be connected between each device node and
ground which is similar from an electrical point of view but improves diagonal
dominance compared to a shunt conductance. In addition, the exponential
characteristic is replaced by a linear characteristic for bias voltages
smaller than a few VT. Although the above mentioned precautions are
guided by numerical reasoning it should be noticed that they do not have any
negative impact on the value of the solution as they might as well be
justified on physical grounds.
0 which could result in a singular matrix. To prevent this occurrence
a small leakage conductance
Gmin of typically
10-9-
10-12 S is placed in shunt with each junction.
Alternatively
Gmin can be connected between each device node and
ground which is similar from an electrical point of view but improves diagonal
dominance compared to a shunt conductance. In addition, the exponential
characteristic is replaced by a linear characteristic for bias voltages
smaller than a few VT. Although the above mentioned precautions are
guided by numerical reasoning it should be noticed that they do not have any
negative impact on the value of the solution as they might as well be
justified on physical grounds.



Next: 6.2.5 The New Method
Up: 6.2 Circuit Equation Damping
Previous: 6.2.3 Global Damping Strategy
Tibor Grasser
1999-05-31