2.1.1 POISSON's Equation

By introducing a vector potential and a scalar potential MAXWELL's equations can often be rewritten in a more practical form. The vector potential 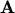$\ensuremath{\boldsymbol{\mathrm{A}}}$ is defined by

$$\ensuremath{\boldsymbol{\mathrm{B}}}= \ensuremath{\ensuremath{\en... ...l{\mathrm{\nabla}}}}\ensuremath{\times}\ensuremath{\boldsymbol{\mathrm{A}}}}\ ,$$ (2.7)

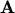which fulfills eqn. (2.2) since $\ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}}}}\ensuremath{... ...athrm{\nabla}}}}\ensuremath{\times}\ensuremath{\boldsymbol{\mathrm{A}}}}\bigr)}$ evaluates to zero for every vector field $\ensuremath{\boldsymbol{\mathrm{A}}}$. Inserting eqn. (2.7) into eqn. (2.1) gives

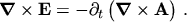$$\ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}}}... ...rm{\nabla}}}}\ensuremath{\times}\ensuremath{\boldsymbol{\mathrm{A}}}}\bigr)}\ .$$ (2.8)

Interchanging the order of the time derivative and the curl operator,

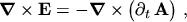$$\ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}}}... ...igl(\ensuremath{\partial_{t} \, \ensuremath{\boldsymbol{\mathrm{A}}}}\bigr)}\ ,$$ (2.9)

and using the associative property of the curl operator,

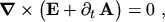$$\ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}}}... ...\ensuremath{\partial_{t} \, \ensuremath{\boldsymbol{\mathrm{A}}}}\bigr)}= 0 \ ,$$ (2.10)

the argument of the curl operator can be substituted by the gradient of a scalar potential

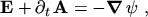$$\ensuremath{\boldsymbol{\mathrm{E}}}+ \ensuremath{\partial_{t} \,... ... \ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}}}}\, \psi}}\ ,$$ (2.11)

since 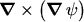$\ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}}}}\ensuremath{... ...nsuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}}}}\, \psi}\bigr)}$ yields zero for every scalar field $\psi$. The minus sign on the right hand side of eqn. (2.11) is introduced by convention based on historical reasons.

In the quasi-stationary case, which holds true for semiconductor devices^2.1, the time derivative of the vector potential can be neglected

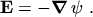$$\ensuremath{\boldsymbol{\mathrm{E}}}= - \ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}}}}\, \psi}\ .$$ (2.12)

POISSON's equation is finally obtained by inserting eqn. (2.12) into eqn. (2.5)

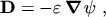$$\ensuremath{\boldsymbol{\mathrm{D}}}= - \varepsilon \, \ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}}}}\, \psi}\ ,$$ (2.13)

which is in turn inserted into eqn. (2.4)

$$\boxed{\ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\n... ...{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}}}}\, \psi}}= - \varrho}\ .$$ (2.14)

In the case of vanishing space charge density $\rho$ POISSON's equation simplifies to the LAPLACE equation

$$\ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}}}... ...suremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}}}}\, \psi}}= 0 \ .$$ (2.15)

M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF