previous up next Dissertation Markus Gritsch contents
 Previous: 2.3.2.1 Gradient Calculation   Up: 2.3.2 Moments Method   Next: 2.3.2.3 Isotropic Distribution Function

2.3.2.2 Macroscopic Relaxation Time Approximation

The collision term on the right hand side of eqns. (2.53) and (2.54), which represents the various scattering processes, can be deliberately modeled as

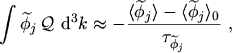$\displaystyle \ensuremath{\int \ensuremath{\widetilde{\phi}}_j \, \mathcal{Q} \... ...ath{\widetilde{\phi}}_j \rangle}_0}{\tau_{\ensuremath{\widetilde{\phi}}_j}} \ ,$ (2.70)

which is commonly termed as relaxation time approximation [14, p.144]. This equation implies that the perturbed distribution function will relax exponentially to the equilibrium function with one time constant $ \tau_{\ensuremath{\widetilde{\phi}}_j}$ when the perturbing field is removed. A discussion on the validity of this approximation is given in [20, p.139].

The equilibrium distribution function $ f_0(\ensuremath{\boldsymbol{\mathrm{k}}})$ is a symmetric function. Since the even weight functions are symmetric in $ \ensuremath{\boldsymbol{\mathrm{k}}}$ and the odd weight functions are anti-symmetric in $ \ensuremath{\boldsymbol{\mathrm{k}}}$, only the even moments of the equilibrium distribution function will be non-zero whereas the odd moments will vanish

$\displaystyle \ensuremath{\langle \phi_j \rangle}_0$ $\displaystyle = \ensuremath{\int \phi_j(k) \, f_0(k) \,\, \ensuremath{\mathrm{d}}^3 k}$   $\displaystyle \neq 0 \textcolor{lightgrey}{.......}\textrm{for even $j$} \ ,$ (2.71)
$\displaystyle \ensuremath{\langle \ensuremath{\boldsymbol{\mathrm{\phi}}}_j \rangle}_0$ $\displaystyle = \ensuremath{\int \ensuremath{\boldsymbol{\mathrm{\phi}}}_j(\ens... ... \, f_0(\ensuremath{\boldsymbol{\mathrm{k}}}) \,\, \ensuremath{\mathrm{d}}^3 k}$   $\displaystyle = 0 \textcolor{lightgrey}{.......}\textrm{for odd $j$} \ .$ (2.72)

Applying the relaxation time approximation and inserting the calculated gradients from the previous section into eqns. (2.53) and (2.54) leads to the equation set

  $\displaystyle \phi_0:$ $\displaystyle \textcolor{lightgrey}{.......}$ $\displaystyle \ensuremath{\partial_{t} \, \ensuremath{\langle 1 \rangle}}$   $\displaystyle + \ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}... ...remath{\cdot}\ensuremath{\langle \ensuremath{\boldsymbol{\mathrm{v}}} \rangle}}$       $\displaystyle =$   $\displaystyle - R \ ,$ (2.73)
  $\displaystyle \phi_2:$ $\displaystyle \textcolor{lightgrey}{.......}$ $\displaystyle \ensuremath{\partial_{t} \, \ensuremath{\langle \mathcal{E} \rangle}}$   $\displaystyle + \ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}... ...nsuremath{\langle \ensuremath{\boldsymbol{\mathrm{v}}} \, \mathcal{E} \rangle}}$   $\displaystyle + \mathrm{q}\, \ensuremath{\boldsymbol{\mathrm{E}}}\ensuremath{\cdot}\ensuremath{\langle \ensuremath{\boldsymbol{\mathrm{v}}} \rangle}$   $\displaystyle = - \frac{\ensuremath{\langle \mathcal{E} \rangle}- \ensuremath{\langle \mathcal{E} \rangle}_0}{\tau_\mathcal{E}}$   $\displaystyle + G_{\mathcal{E}\, n} \ ,$ (2.74)
  $\displaystyle \phi_4:$ $\displaystyle \textcolor{lightgrey}{.......}$ $\displaystyle \ensuremath{\partial_{t} \, \ensuremath{\langle v^2 \, \mathcal{E} \rangle}}$   $\displaystyle + \ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}... ...th{\langle \ensuremath{\boldsymbol{\mathrm{v}}} \, v^2 \, \mathcal{E} \rangle}}$   $\displaystyle + \frac{4 \, \mathrm{q}}{m} \, \ensuremath{\boldsymbol{\mathrm{E}... ...ensuremath{\langle \ensuremath{\boldsymbol{\mathrm{v}}} \, \mathcal{E} \rangle}$   $\displaystyle = - \frac{\ensuremath{\langle v^2 \, \mathcal{E} \rangle}- \ensuremath{\langle v^2 \, \mathcal{E} \rangle}_0}{\tau_\beta}$   $\displaystyle + G_{\beta \, n} \ ,$ (2.75)

  $\displaystyle \ensuremath{\boldsymbol{\mathrm{\phi}}}_1:$ $\displaystyle \textcolor{lightgrey}{.......}$ $\displaystyle \ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}}}... ...\mathrm{v}}} \ensuremath{\otimes}\ensuremath{\boldsymbol{\mathrm{p}}} \rangle}}$   $\displaystyle + \mathrm{q}\, \ensuremath{\boldsymbol{\mathrm{E}}}\ensuremath{\cdot}\ensuremath{\langle \ensuremath{\widetilde{\delta}} \rangle}$   $\displaystyle = - \frac{\ensuremath{\langle \ensuremath{\boldsymbol{\mathrm{p}}} \rangle}}{\tau_m} \ ,$ (2.76)
  $\displaystyle \ensuremath{\boldsymbol{\mathrm{\phi}}}_3:$ $\displaystyle \textcolor{lightgrey}{.......}$ $\displaystyle \ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}}}... ...nsuremath{\otimes}\ensuremath{\boldsymbol{\mathrm{v}}} \, \mathcal{E} \rangle}}$   $\displaystyle + \mathrm{q}\, \ensuremath{\boldsymbol{\mathrm{E}}}\ensuremath{\c... ...{\mathrm{v}}} \ensuremath{\otimes}\ensuremath{\boldsymbol{\mathrm{v}}} \rangle}$   $\displaystyle = - \frac{\ensuremath{\langle \ensuremath{\boldsymbol{\mathrm{v}}} \, \mathcal{E} \rangle}}{\tau_S} \ ,$ (2.77)
  $\displaystyle \ensuremath{\boldsymbol{\mathrm{\phi}}}_5:$ $\displaystyle \textcolor{lightgrey}{.......}$ $\displaystyle \ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}}}... ...th{\otimes}\ensuremath{\boldsymbol{\mathrm{v}}} \, v^2 \, \mathcal{E} \rangle}}$   $\displaystyle + \frac{\mathrm{q}}{m} \, \ensuremath{\boldsymbol{\mathrm{E}}}\en... ...\mathrm{v}}} \ensuremath{\otimes}\ensuremath{\boldsymbol{\mathrm{v}}}) \rangle}$   $\displaystyle = - \frac{\ensuremath{\langle \ensuremath{\boldsymbol{\mathrm{v}}} \, v^2 \, \mathcal{E} \rangle}}{\tau_K} \ ,$ (2.78)

where $ \tau_m$, $ \tau_\mathcal{E}$, $ \tau_S$, $ \tau_\beta$, $ \tau_K$ are the relaxation times for momentum, energy, energy flux density, kurtosis, and kurtosis flux density, respectively.


previous up next   contents
 Previous: 2.3.2.1 Gradient Calculation   Up: 2.3.2 Moments Method   Next: 2.3.2.3 Isotropic Distribution Function
M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF