previous up next Dissertation Markus Gritsch contents
 Previous: 2.3.1 BOLTZMANN's Transport Equation   Up: 2.3 Systematic Approach   Next: 2.3.2.1 Gradient Calculation

2.3.2 Moments Method

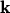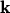General schemes to derive transport models from BTE have been proposed by Stratton [16] and Bløtekjær [17]. The moments method is characterized by multiplying each term of BTE with a weight function and integrate the whole equation over $ \ensuremath{\boldsymbol{\mathrm{k}}}$-space2.4. By this procedure the coordinates of the $ \ensuremath{\boldsymbol{\mathrm{k}}}$-space are saturated and a set of differential equations in ( $ \ensuremath{\boldsymbol{\mathrm{r}}}$, t)-space is left. Consequently, some information originally carried by the distribution function is lost. However, in many practical cases the information retained by the equations in ( $ \ensuremath{\boldsymbol{\mathrm{r}}}$, t)-space is sufficient to capture the essential features of the problem at hand [18, p.112]. The moments of the distribution function are defined by

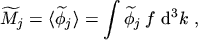$\displaystyle \ensuremath{\widetilde{M}}_j = \ensuremath{\langle \ensuremath{\w... ...{\int \ensuremath{\widetilde{\phi}}_j \, f \,\, \ensuremath{\mathrm{d}}^3 k}\ ,$ (2.44)

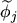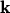where $ \ensuremath{\widetilde{\phi}}_j$ denotes a weight function which can either be of scalar or vectorial type. The weight functions are usually chosen as powers of increasing order of the vector $ \ensuremath{\boldsymbol{\mathrm{k}}}$. These powers are accompanied by some appropriate scaling factors to get physically meaningful quantities. In this work moments up to the sixth order will be considered. The corresponding weight functions for the even orders read

$\displaystyle \phi_0$ $\displaystyle = 1 \ ,$     (2.45)
$\displaystyle \phi_2$ $\displaystyle = \mathcal{E}$   $\displaystyle = \frac{\hbar^2 \, k^2}{2 \, m} \ ,$ (2.46)
$\displaystyle \phi_4$ $\displaystyle = v^2 \, \mathcal{E}$   $\displaystyle = \frac{\hbar^4 \, k^4}{2 \, m^3} \ ,$ (2.47)
$\displaystyle \phi_6$ $\displaystyle = v^4 \, \mathcal{E}$   $\displaystyle = \frac{\hbar^6 \, k^6}{2 \, m^5} \ ,$ (2.48)

and the weight functions for the odd orders are

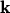$\displaystyle \ensuremath{\boldsymbol{\mathrm{\phi}}}_1$ $\displaystyle = \ensuremath{\boldsymbol{\mathrm{p}}}$   $\displaystyle = \hbar \, \ensuremath{\boldsymbol{\mathrm{k}}}\ ,$ (2.49)
$\displaystyle \ensuremath{\boldsymbol{\mathrm{\phi}}}_3$ $\displaystyle = \ensuremath{\boldsymbol{\mathrm{v}}}\, \mathcal{E}$   $\displaystyle = \frac{\hbar^3 \, k^2 \, \ensuremath{\boldsymbol{\mathrm{k}}}}{2 \, m^2} \ ,$ (2.50)
$\displaystyle \ensuremath{\boldsymbol{\mathrm{\phi}}}_5$ $\displaystyle = \ensuremath{\boldsymbol{\mathrm{v}}}\, v^2 \, \mathcal{E}$   $\displaystyle = \frac{\hbar^5 \, k^4 \, \ensuremath{\boldsymbol{\mathrm{k}}}}{2 \, m^4} \ ,$ (2.51)

where $ \ensuremath{\boldsymbol{\mathrm{p}}}$ is the momentum, $ \hbar$ is the reduced PLANCK constant, $ \ensuremath{\boldsymbol{\mathrm{k}}}$ is the wave vector, 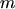$ m$ is the effective mass2.5, and 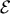$ \mathcal{E}$ is the energy. It is to note that the weight functions of even orders are scalars whereas the odd orders yield vectorial forms. As will be seen later, using these weight functions in the moments method the even orders will lead to the balance equations whereas the odd orders will lead to the flux equations.

In eqns. (2.46) to (2.51) a single effective parabolic energy band has been assumed2.6:

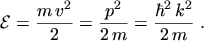$\displaystyle \mathcal{E}= \frac{m \, v^2}{2} = \frac{p^2}{2 \, m} = \frac{\hbar^2 \, k^2}{2 \, m} \ .$ (2.52)

The following derivation will be carried out only for electrons for the sake of clarity and brevity. As the derivation for holes is analogous, the results for holes will be presented without derivation. Applying the moments method to BTE the moment equations for electrons are obtained

$\displaystyle \ensuremath{\partial_{t} \, \ensuremath{\langle \phi_j \rangle}}$ $\displaystyle + \ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}... ...ot}\ensuremath{\langle \ensuremath{\boldsymbol{\mathrm{v}}} \, \phi_j \rangle}}$   $\displaystyle + \mathrm{q}\, \ensuremath{\boldsymbol{\mathrm{E}}}\ensuremath{\c... ...\ensuremath{\boldsymbol{\mathrm{\nabla}}}_{\negmedspace p}} \, \phi_j} \rangle}$   $\displaystyle = \ensuremath{\int \phi_j \, \mathcal{Q} \,\, \ensuremath{\mathrm{d}}^3 k}$   $\displaystyle - \ensuremath{\int \phi_j \, \mathcal{R} \,\, \ensuremath{\mathrm{d}}^3 k}\ ,$ $\displaystyle \textcolor{lightgrey}{....}$ $\displaystyle \textrm{$j$\ even} \ , \hspace{-3em}$ (2.53)
$\displaystyle \ensuremath{\partial_{t} \, \ensuremath{\langle \ensuremath{\boldsymbol{\mathrm{\phi}}}_j \rangle}}$ $\displaystyle + \ensuremath{\ensuremath{\ensuremath{\boldsymbol{\mathrm{\nabla}... ...rm{v}}} \ensuremath{\otimes}\ensuremath{\boldsymbol{\mathrm{\phi}}}_j \rangle}}$   $\displaystyle + \mathrm{q}\, \ensuremath{\boldsymbol{\mathrm{E}}}\ensuremath{\c... ...}_{\negmedspace p}} \otimes \ensuremath{\boldsymbol{\mathrm{\phi}}}_j} \rangle}$   $\displaystyle = \ensuremath{\int \ensuremath{\boldsymbol{\mathrm{\phi}}}_j \, \mathcal{Q} \,\, \ensuremath{\mathrm{d}}^3 k}$   $\displaystyle - \ensuremath{\int \ensuremath{\boldsymbol{\mathrm{\phi}}}_j \, \mathcal{R} \,\, \ensuremath{\mathrm{d}}^3 k}\ ,$ $\displaystyle \textcolor{lightgrey}{....}$ $\displaystyle \textrm{$j$\ odd} \ . \hspace{-3em}$ (2.54)


Subsections


previous up next   contents
 Previous: 2.3.1 BOLTZMANN's Transport Equation   Up: 2.3 Systematic Approach   Next: 2.3.2.1 Gradient Calculation
M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF