Eqns. (2.76) to (2.78) all contain a
statistical average of a symmetric tensor (see Appendix A) of the
form
 which will be evaluated in this section. The
distribution function can be decomposed into a symmetric and an anti-symmetric part
which will be evaluated in this section. The
distribution function can be decomposed into a symmetric and an anti-symmetric part
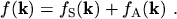 |
(2.79) |
In this section we assume that the symmetric part is isotropic
 |
(2.80) |
This is a special case of the diffusion approximation [21, p.49] which will be explained in more detail for the
MAXWELL distribution in Section 2.3.3.1 on
page ![[*]](./crossref.png) . By using this assumption the statistical average
of the tensor can be written as
. By using this assumption the statistical average
of the tensor can be written as
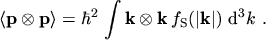 |
(2.81) |
For symmetry reasons all elements outside the trace vanish. For instance, the element
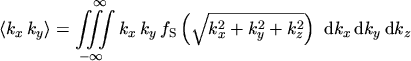 |
(2.82) |
evaluates to zero because of the integral
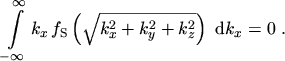 |
(2.83) |
Since the distribution function is assumed to be isotropic, the integrals determining the elements of the
trace all evaluate to a common value 
 |
(2.84) |
The value of  can be evaluated by the simple transformation
can be evaluated by the simple transformation
Therefore, the statistical averages of the tensors are diagonal with all diagonal elements
being equal:
By inserting eqns. (2.88) and (2.89) into
eqns. (2.76) to (2.78) one gets
Note that the divergences of the tensors simplify to gradients of scalars.
M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF
![[*]](./crossref.png) . By using this assumption the statistical average
of the tensor can be written as
. By using this assumption the statistical average
of the tensor can be written as
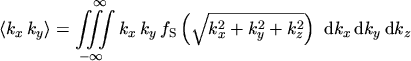
![]()
