|
|
|
|
Previous: 2.3.3 Closure Up: 2.3.3 Closure Next: 2.3.3.2 Discussion of the Diffusion Approximation |
| (2.105) |
An example of a shifted MAXWELLian distribution function together with its symmetric and anti-symmetric part is depicted in Fig. 2.1.
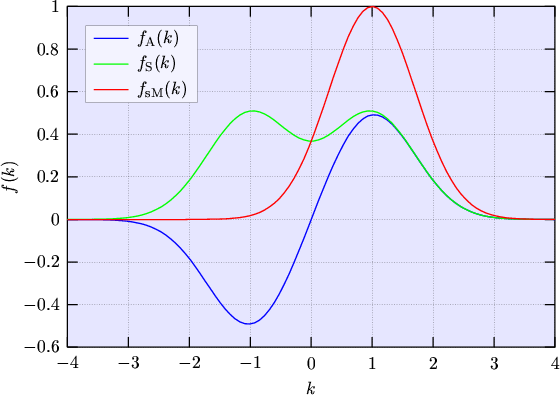 |
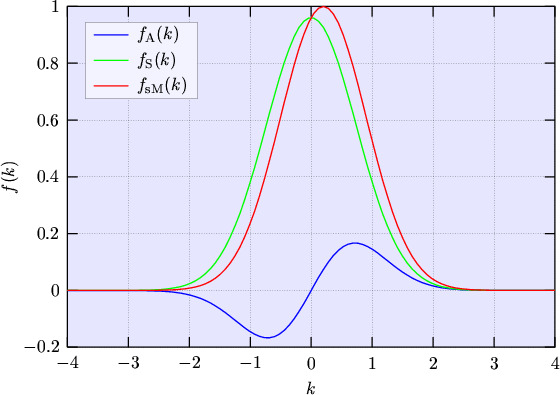
The diffusion approximation now assumes that the displacement of the distribution function is small which means that the anti-symmetric part is much smaller than the symmetric one. Then it is justified to approximate the shifted MAXWELL distribution function by a series expansion with respect to the displacement and to truncate the expansion after the first term:
| (2.109) | ||
| (2.110) | ||
| (2.111) |
 |
 |
The interpretation of eqn. (2.111) is that the symmetric part can be approximated by a non-displaced MAXWELL distribution function
For closing the moment equation system at even moments, an assumption about the symmetric part
of the distribution function must be introduced since the integrals of even powers of
![]() multiplied with the anti-symmetric part vanish. Vice versa, for closing the moment
equation system at odd moments, only the anti-symmetric part of the distribution function must
be assumed since the integrals of odd powers of
multiplied with the anti-symmetric part vanish. Vice versa, for closing the moment
equation system at odd moments, only the anti-symmetric part of the distribution function must
be assumed since the integrals of odd powers of
![]() multiplied with the symmetric part
vanish.
multiplied with the symmetric part
vanish.
The even moments will be calculated as powers of the energy
![]() since for
parabolic bands
since for
parabolic bands
![]() and
and
![]() only differ by a constant
prefactor
only differ by a constant
prefactor ![]() . The same holds true for
. The same holds true for
![]() and
and
![]() where
the constant prefactor yields
where
the constant prefactor yields ![]() . Starting from
. Starting from
 |
(2.114) |
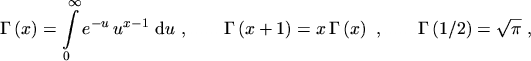 |
(2.117) |
| (2.119) | ||
| (2.120) | ||
| (2.121) | ||
| (2.122) |
M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF