3.3.1 POISSON's Equation

To find a discrete approximation of MAXWELL's fourth equation, eqn. (2.4) is integrated over a control volume $\ensuremath{\mathcal{ V }}_i$

$\displaystyle \ensuremath{\int_{\ensuremath{\mathcal{ V }}_i} \ensuremath{\ensu... ...h{\int_{\ensuremath{\mathcal{ V }}_i} \varrho \,\, \ensuremath{\mathrm{d}}V}\ .$

(3.18)

Applying the theorem of GAUSS to the left hand side turns eqn. (3.18) into

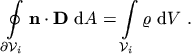$\displaystyle \ensuremath{\oint_{\partial \ensuremath{\mathcal{ V }}_i} \ensure... ...h{\int_{\ensuremath{\mathcal{ V }}_i} \varrho \,\, \ensuremath{\mathrm{d}}V}\ .$

(3.19)

The integrals are approximated as follows:

$\displaystyle \sum_j \, D_{ij} \, A_{ij} = \varrho_i V_i \ ,$

(3.20)

where $D_{ij}$ is the projection of the flux $\ensuremath{\boldsymbol{\mathrm{D}}}$ onto the grid edge $d_{ij}$ , evaluated at the midpoint of the edge, $A_{ij}$ is the boundary line which belongs to both subdomains $\ensuremath{\mathcal{ V }}_i$ and $\ensuremath{\mathcal{ V }}_j$ , and $\varrho_i$ is the space charge density at the grid point

(Fig. 3.4).

**Figure 3.4:** Control volume of grid point used for the box integration method.
$\includegraphics[width=.5\textwidth]{eps/ControlVolume.eps}$

The remaining task is to find an approximation for the projection of the dielectric flux density $D_{ij}$ . This is done by the finite difference approximation

$\displaystyle D_{ij}$	$\displaystyle = - \varepsilon \, \frac{\psi_j - \psi_i}{d_{ij}} \ ,$	(3.21)
$\displaystyle \varepsilon$	$\displaystyle = \frac{\varepsilon_i + \varepsilon_j}{2} \ .$	(3.22)

With eqn. (3.20) and eqn. (3.21), the discretization of POISSON's equation can be concluded.

M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF


Previous: 3.3 Box Integration Method Up: 3.3 Box Integration Method Next: 3.3.2 Six Moments Transport Model