|
|
|
|
Previous: 3.2.3 Final Remarks Up: 3. Discretization Next: 3.3.1 POISSON's Equation |
![\includegraphics[width=.5\textwidth]{eps/VoronoiExample.eps}](img764.png) |
The subdomains are also called VORONOI3.2 regions. A VORONOI region is defined as the set of all points that are closer to the considered grid point than to any other grid point. The differential equations are then integrated over each of the subdomains and discretized by approximating the integrals by numerical integration rules.
For an orthogonal grid structure the box integration method leads to the expressions obtained from the finite difference method.
To get a connection between the global and the local attributes of fields, a relation between the integral over a domain and the boundary of this domain must be presented. Its general form is the GREEN transformation
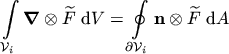 |
(3.16) |