3. Grundlagen der Feldberechnung

In diesem Kapitel werden die physikalischen Zusammenhänge wiedergegeben, die durch partielle Differentialgleichungen und Randbedingungen bestimmt sind. Die Grundlagen der klassischen Elektrodynamik bilden die Maxwell-Gleichungen

$$\nabla\!\times\!\mathchoice{\mbox{\boldmath$\displaystyle H$}} {\... ...$}} {\mbox{\boldmath$\scriptstyle H$}} {\mbox{\boldmath$\scriptscriptstyle H$}} =\mathchoice{\mbox{\boldmath$\displaystyle J$}} {\mbox{\boldmath$... ...math$\scriptstyle D$}} {\mbox{\boldmath$\scriptscriptstyle D$}}}}{\partial{t}},$$ (3.1)

$$\nabla\!\times\!\mathchoice{\mbox{\boldmath$\displaystyle E$}} {\... ...$}} {\mbox{\boldmath$\scriptstyle E$}} {\mbox{\boldmath$\scriptscriptstyle E$}} =-\frac{\partial{\mathchoice{\mbox{\boldmath$\displaystyle B$}} {... ...math$\scriptstyle B$}} {\mbox{\boldmath$\scriptscriptstyle B$}}}}{\partial{t}},$$ (3.2)

$$\nabla\!\cdot\!\mathchoice{\mbox{\boldmath$\displaystyle D$}} {\m... ...$}} {\mbox{\boldmath$\scriptstyle D$}} {\mbox{\boldmath$\scriptscriptstyle D$}} =\rho,$$ (3.3)

$$\nabla\!\cdot\!\mathchoice{\mbox{\boldmath$\displaystyle B$}} {\m... ...$}} {\mbox{\boldmath$\scriptstyle B$}} {\mbox{\boldmath$\scriptscriptstyle B$}} =0$$ (3.4)

und die Materialgleichungen

$$\mathchoice{\mbox{\boldmath$\displaystyle B$}} {\mbox{\boldmath$\... ...$}} {\mbox{\boldmath$\scriptstyle B$}} {\mbox{\boldmath$\scriptscriptstyle B$}} = \mu\mathchoice{\mbox{\boldmath$\displaystyle H$}} {\mbox{\boldm... ...}} {\mbox{\boldmath$\scriptstyle H$}} {\mbox{\boldmath$\scriptscriptstyle H$}},$$ (3.5)

$$\mathchoice{\mbox{\boldmath$\displaystyle D$}} {\mbox{\boldmath$\... ...$}} {\mbox{\boldmath$\scriptstyle D$}} {\mbox{\boldmath$\scriptscriptstyle D$}} = \makebox{\boldmath$\varepsilon$}\mathchoice{\mbox{\boldmath$\di... ...}} {\mbox{\boldmath$\scriptstyle E$}} {\mbox{\boldmath$\scriptscriptstyle E$}},$$ (3.6)

$$\mathchoice{\mbox{\boldmath$\displaystyle J$}} {\mbox{\boldmath$\... ...$}} {\mbox{\boldmath$\scriptstyle J$}} {\mbox{\boldmath$\scriptscriptstyle J$}} = \gamma\mathchoice{\mbox{\boldmath$\displaystyle E$}} {\mbox{\bo... ...}} {\mbox{\boldmath$\scriptstyle E$}} {\mbox{\boldmath$\scriptscriptstyle E$}}.$$ (3.7)

Die Materialparameter sind die magnetische Permeabilität $\mu$, die elektrische Permittivität $\makebox{\boldmath $\varepsilon$}$, und die elektrische Leitfähigkeit $\gamma$. Die magnetische Permeabilität $\mu$ wird als konstant angenommen, da keine magnetischen Materialien behandelt werden. Global erfolgen die Verknüpfungen (3.5, 3.6) über die wesentlich geometrieabhängigen Kapazitäts- bzw. Induktivitätskoeffizienten.

Potenzialformulierungen erweisen sich häufig als günstig, da sie zur Reduktion der Anzahl der Feldvariablen führen. Der Ansatz

$$\mathchoice{\mbox{\boldmath$\displaystyle B$}} {\mbox{\boldmath$\... ...$}} {\mbox{\boldmath$\scriptstyle B$}} {\mbox{\boldmath$\scriptscriptstyle B$}} =\nabla\!\times\!\mathchoice{\mbox{\boldmath$\displaystyle A$}} {... ...$}} {\mbox{\boldmath$\scriptstyle A$}} {\mbox{\boldmath$\scriptscriptstyle A$}}$$ (3.8)

mit dem magnetischen Vektorpotenzial  $\mathchoice{\mbox{\boldmath $\displaystyle A$}} {\mbox{\boldmath $\textstyle A$}} {\mbox{\boldmath $\scriptstyle A$}} {\mbox{\boldmath $\scriptscriptstyle A$}}$ löst formal (3.4) für beliebige Vektorfelder. Damit folgt aus (3.2) mit dem Skalarpotenzial $\varphi$ für die elektrische Feldstärke

$$\mathchoice{\mbox{\boldmath$\displaystyle E$}} {\mbox{\boldmath$\... ...A$}} {\mbox{\boldmath$\scriptscriptstyle A$}}}}{\partial{t}}-\nabla\!\varphi\,.$$ (3.9)

Durch die Einführung der Potenziale $\mathchoice{\mbox{\boldmath $\displaystyle A$}} {\mbox{\boldmath $\textstyle A$}} {\mbox{\boldmath $\scriptstyle A$}} {\mbox{\boldmath $\scriptscriptstyle A$}}$, $\varphi$ sind die Felder $\mathchoice{\mbox{\boldmath $\displaystyle E$}} {\mbox{\boldmath $\textstyle E$}} {\mbox{\boldmath $\scriptstyle E$}} {\mbox{\boldmath $\scriptscriptstyle E$}}$, $\mathchoice{\mbox{\boldmath $\displaystyle B$}} {\mbox{\boldmath $\textstyle B$}} {\mbox{\boldmath $\scriptstyle B$}} {\mbox{\boldmath $\scriptscriptstyle B$}}$ eindeutig festgelegt, allerdings gilt nicht die Umkehrung, da die Änderung der Potenziale mit einem hinreichend glatten, beliebigen Skalarfeld $C$ die gleichen Felder $\mathchoice{\mbox{\boldmath $\displaystyle E$}} {\mbox{\boldmath $\textstyle E$}} {\mbox{\boldmath $\scriptstyle E$}} {\mbox{\boldmath $\scriptscriptstyle E$}}$, $\mathchoice{\mbox{\boldmath $\displaystyle B$}} {\mbox{\boldmath $\textstyle B$}} {\mbox{\boldmath $\scriptstyle B$}} {\mbox{\boldmath $\scriptscriptstyle B$}}$ ergeben

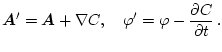$$\mathchoice{\mbox{\boldmath$\displaystyle A$}} {\mbox{\boldmath$\... ...style A$}}+\nabla{C}, \quad \varphi'=\varphi-\frac{\partial{C}}{\partial{t}}\,.$$ (3.10)

Zur eindeutigen Festlegung des Vektorpotenzials $\mathchoice{\mbox{\boldmath $\displaystyle A$}} {\mbox{\boldmath $\textstyle A$}} {\mbox{\boldmath $\scriptstyle A$}} {\mbox{\boldmath $\scriptscriptstyle A$}}$ ist noch eine Aussage über die Quellen dieses Feldes zu treffen. Zwei Eichtransformationen haben sich als besonders vorteilhaft herausgestellt, nämlich die Lorentz-Eichung und die Coulomb-Eichung.

Die Lorentz-Eichung führt zu zwei entkoppelten Wellengleichungen, deren partikuläre Lösung durch retardierte (verzögerte) Potenziale dargestellt wird. Dann errechnen sich das Potenzial $\varphi$ und das Vektorpotenzial $\mathchoice{\mbox{\boldmath $\displaystyle A$}} {\mbox{\boldmath $\textstyle A$}} {\mbox{\boldmath $\scriptstyle A$}} {\mbox{\boldmath $\scriptscriptstyle A$}}$ nicht aus den derzeitigen Werten, sondern aus früheren [75,76]. Die Coulomb-Eichung führt auf eine Poisson-Gleichung für das Skalarpotenzial und für das Vektorpotenzial auf eine Vektor-Poisson-Gleichung, wie im folgenden Abschnitt gezeigt wird.