Unterabschnitte
Von quasistatischer Näherung spricht man, wenn der Verschiebungstrom
gegenüber dem Leitungsstrom vernachlässigt wird.
Dadurch vereinfachen sich die Maxwell-Gleichungen signifikant, (3.1)
reduziert sich zu
Basierend auf dem Ansatz (3.8) erhält man unter Verwendung der Sätze der
Vektoranalysis
Damit folgt aus (3.11)
sowie unter der Einbeziehung von (3.5)
Aus (3.3) und der Materialgleichung (3.6) folgt
Bei Einführung der Coulomb-Eichung
wird (3.14) zu
und (3.13)
Diese Poisson-Gleichungen können mithilfe der Green-Funktionen3.1 gelöst werden:
In der quasistatischen Näherung erscheint die Wellenausbreitungsgeschwindigkeit
unendlich, daher zeigt diese Näherung nur gute Resultate, wenn die
minimale Wellenlänge des ausbreitenden Signals wesentlich größer
als die Abmessungen des Leitungssystems senkrecht zur Ausbreitungsrichtung
ist3.2 [2,77].
Die Lösungen sind
Außerdem sind in dieser Näherung das elektrische und das magnetische Feld
entkoppelt. Im allgemeinen zeitabhängigen Fall sind elektrisches und
magnetisches Feld immer gekoppelt, siehe (3.1) und (3.2).
Wenn aber die Kopplung vernachlässigbar wird, kann man das elektrische und das magnetische Feld unabhängig voneinander berechnen.
Aus (3.2) folgt im stationären Zustand (
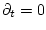 ),
dass das elektrische Feld aus dem Gradienten eines skalaren Potenzials
berechnet werden kann
),
dass das elektrische Feld aus dem Gradienten eines skalaren Potenzials
berechnet werden kann
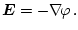 |
(3.21) |
Für den stationären Fall mit linearer Dielektrizitätszahl ist das
Verhältnis von Ladung 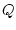 und Spannung
und Spannung 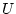 zweier voneinander isolierter
Leiter konstant und wird als Kapazität
zweier voneinander isolierter
Leiter konstant und wird als Kapazität 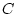 bezeichnet
bezeichnet
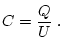 |
(3.22) |
Da die Leiter im Inneren feldfrei sind, ist das Potenzial im ganzen Leiter
konstant und die Ladung ist ausschließlich auf der Oberfläche der Leiter
verteilt.
Die Ladungsverteilung ergibt sich aus der elektrischen Flussdichte
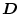 gemäß der dritten Maxwellschen Gleichung (3.3).
Betrachtet man einen die Oberfläche eines Leiters umgebenden Bereich mit
der Dicke
gemäß der dritten Maxwellschen Gleichung (3.3).
Betrachtet man einen die Oberfläche eines Leiters umgebenden Bereich mit
der Dicke 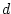 und lässt
und lässt 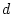 gegen Null gehen, so erhält man die
Flächenladungsdichte
gegen Null gehen, so erhält man die
Flächenladungsdichte 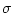 als Differenz der Normalkomponenten von
als Differenz der Normalkomponenten von
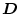 außerhalb (
außerhalb (
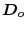 ) und innerhalb (
) und innerhalb (
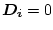 ) des
Leiters
) des
Leiters
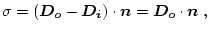 |
(3.23) |
wobei der Vektor
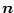 normal auf die Leiteroberfläche steht und in
Richtung Dielektrikum zeigt. Mittels Ladungsintegration über die
Leiteroberfläche
normal auf die Leiteroberfläche steht und in
Richtung Dielektrikum zeigt. Mittels Ladungsintegration über die
Leiteroberfläche 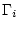
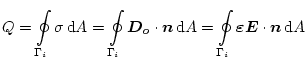 |
(3.24) |
kann man die gesamte auf einem Leiter gespeicherte Ladung berechnen.
Über (3.22) lässt sich daraus die Kapazität zwischen zwei Leitern
ermitteln3.3.
Als Alternative zur Ladungsintegration kann die Kapazität auch mit der
Energiemethode ermittelt werden.
Die in einem Kondensator gespeicherte Energie 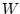 lässt sich durch
lässt sich durch
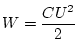 |
(3.25) |
ausdrücken, die natürlich gleich der im elektrischen Feld enthaltenen
Energie
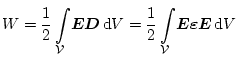 |
(3.26) |
sein muss.
Der Integrationsbereich 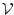 erstreckt sich über das gesamte
Dielektrikum zwischen den Leitern und geht theoretisch i.a. bis ins
Unendliche. Das elektrische Feld ladungsbalancierter Leiter klingt für
Entfernungen, die groß gegenüber dem Durchmesser des Gebietes sind, das
die Ladungen enthält, mit der dritten Potenz des mittleren Abstands ab.
Deshalb ist der größte Teil der Feldenergie in der nächsten Umgebung
der Leiter enthalten und der Integrationsbereich kann für praktische
Anwendungen entsprechend verkleinert werden, ohne dass damit ein großer Fehler
bei der Energieberechnung gemacht wird.
erstreckt sich über das gesamte
Dielektrikum zwischen den Leitern und geht theoretisch i.a. bis ins
Unendliche. Das elektrische Feld ladungsbalancierter Leiter klingt für
Entfernungen, die groß gegenüber dem Durchmesser des Gebietes sind, das
die Ladungen enthält, mit der dritten Potenz des mittleren Abstands ab.
Deshalb ist der größte Teil der Feldenergie in der nächsten Umgebung
der Leiter enthalten und der Integrationsbereich kann für praktische
Anwendungen entsprechend verkleinert werden, ohne dass damit ein großer Fehler
bei der Energieberechnung gemacht wird.
Sowohl die Energiemethode als auch das Verfahren der Ladungsintegration
erfordern die numerische Berechnung des elektrischen Feldes.
Anzumerken ist, dass bei der Ladungsintegration die Berechnung des Feldes
auf der Leiteroberfläche genügt.
Setzt man (3.21) in (3.3) ein und berücksichtigt, dass in den
Isolatoren keine elektrischen Ladungen (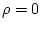 ) vorhanden sind, erhält man
die Euler-Gleichung
) vorhanden sind, erhält man
die Euler-Gleichung
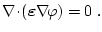 |
(3.27) |
Das Gebiet 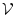 , auf dem Gleichung (3.27) gelöst werden soll, wird
durch mehrere Flächen berandet (Abb. 3.1).
, auf dem Gleichung (3.27) gelöst werden soll, wird
durch mehrere Flächen berandet (Abb. 3.1).
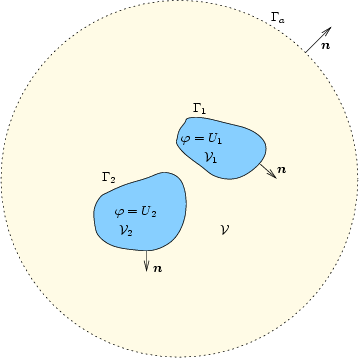
Abbildung 3.1:
Simulationsbereich und Ränder bei der Berechnung des elektrischen Feldes:
Die beiden Elektroden
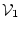 und
und
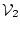 liegen auf konstanten
Potenzialen (
liegen auf konstanten
Potenzialen (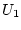 bzw.
bzw. 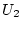 ) und bilden somit Dirichlet-Bedingungen. Der
äußere Rand
) und bilden somit Dirichlet-Bedingungen. Der
äußere Rand  wird durch eine homogene Neumann-Bedingung
modelliert.
wird durch eine homogene Neumann-Bedingung
modelliert.
 |
Die konstanten Potenziale der Leiteroberflächen stellen
Dirichlet-Bedingungen dar
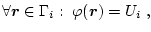 |
(3.28) |
wobei mit 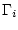 die Oberfläche des Leiters
die Oberfläche des Leiters 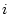 bezeichnet wird.
Wenn man für die numerische Berechnung das Simulationsgebiet nach außen hin
begrenzt, benötigt man auch für
bezeichnet wird.
Wenn man für die numerische Berechnung das Simulationsgebiet nach außen hin
begrenzt, benötigt man auch für 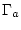 eine Randbedingung, die man
sinnvollerweise so wählt, dass die Oberfläche ladungsfrei bleibt, also
eine Randbedingung, die man
sinnvollerweise so wählt, dass die Oberfläche ladungsfrei bleibt, also
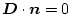 gilt, oder durch das Potenzial ausgedrückt:
gilt, oder durch das Potenzial ausgedrückt:
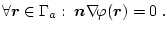 |
(3.29) |
Diese Art von Randbedingung wird homogene Neumann-Bedingung genannt.
Oberflächen, auf denen eine fixe elektrische Flächenladungsdichte 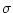 eingeprägt ist, lassen sich durch allgemeine Neumann-Bedingungen
darstellen:
eingeprägt ist, lassen sich durch allgemeine Neumann-Bedingungen
darstellen:
 |
(3.30) |
3.1.2 Elektrischer Strom und Widerstand
Gemäß dem Ohmschen Gesetz ist der elektrische Widerstand eines Leiters im
statischen Fall als das Verhältnis von Klemmenspannung und Strom definiert:
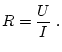 |
(3.31) |
Der Widerstand einer Leitung kann nun berechnet werden, indem man an den Enden
des Leiters eine Spannung anlegt und den Leitungsstrom durch Integration über
eine Kontaktfläche des Leiters 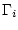 ermittelt
ermittelt
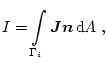 |
(3.32) |
oder man erhält den Widerstand aus der elektrischen Verlustleistung im Leiter
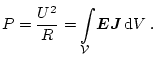 |
(3.33) |
Für die Berechnung des elektrischen Feldes geht man wieder vom zeitlich
unveränderlichen Fall aus und nimmt die elektrische Feldstärke als
reines Gradientenfeld gemäß (3.21) an.
Ferner lässt sich zeigen, dass die Stromdichte
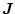 quellenfrei
ist, indem man den Divergenzoperator auf (3.1) anwendet:
quellenfrei
ist, indem man den Divergenzoperator auf (3.1) anwendet:
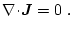 |
(3.34) |
Setzt man nun (3.7) ein, erhält man die folgende
Differentialgleichung für das elektrische Potenzial in einem Leiter
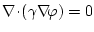 |
(3.35) |
mit der Leitfähigkeit 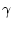 .
Man erkennt, dass diese Gleichung vom gleichen Typ wie (3.27) ist.
Der Bereich
.
Man erkennt, dass diese Gleichung vom gleichen Typ wie (3.27) ist.
Der Bereich 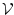 , auf dem (3.35) gelöst werden soll, entspricht
dem Inneren des stromführenden Leiters.
Der Teil der Oberfläche, der ausschließlich von Isolatoren umgeben ist und
keine Kontakte enthält (
, auf dem (3.35) gelöst werden soll, entspricht
dem Inneren des stromführenden Leiters.
Der Teil der Oberfläche, der ausschließlich von Isolatoren umgeben ist und
keine Kontakte enthält (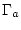 ), stellt für das Potenzial eine
homogene Neumann-Bedingung dar, da kein Strom vom Leiter in den
Isolator fließen kann (
), stellt für das Potenzial eine
homogene Neumann-Bedingung dar, da kein Strom vom Leiter in den
Isolator fließen kann (
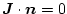 ), und somit gilt:
), und somit gilt:
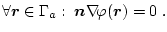 |
(3.36) |
An den Kontaktflächen 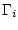 wird üblicherweise ein konstantes
Potenzial
wird üblicherweise ein konstantes
Potenzial 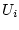 vorgegeben, was eine Dirichlet-Bedingung darstellt:
vorgegeben, was eine Dirichlet-Bedingung darstellt:
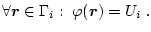 |
(3.37) |
Alternativ zu einem konstanten Potenzial könnte man auch an den Kontakten
eine konstante Stromdichte 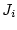 (normal zur Oberfläche) einprägen
(inhomogene Neumann-Bedingung)
(normal zur Oberfläche) einprägen
(inhomogene Neumann-Bedingung)
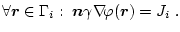 |
(3.38) |
Wenn man hingegen anstatt der Stromdichteverteilung den Gesamtstrom
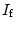 angeben möchte und gleichzeitig ein konstantes Potenzial mit
einem noch unbekannten Wert
angeben möchte und gleichzeitig ein konstantes Potenzial mit
einem noch unbekannten Wert
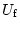 fordert, ergibt das eine
schwebende Randbedingung (``floating boundary condition'')
fordert, ergibt das eine
schwebende Randbedingung (``floating boundary condition'')
Wenn das Gebiet 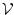 ausschließlich von Neumann-Bedingungen oder
schwebenden Randbedingungen umgeben ist, dann hat (3.35) keine
eindeutige Lösung für das Potenzial.
Durch die Wahl eines beliebigen Potenzialwertes in einem beliebigen Punkt
ausschließlich von Neumann-Bedingungen oder
schwebenden Randbedingungen umgeben ist, dann hat (3.35) keine
eindeutige Lösung für das Potenzial.
Durch die Wahl eines beliebigen Potenzialwertes in einem beliebigen Punkt
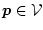 kann die Eindeutigkeit wieder hergestellt werden:
kann die Eindeutigkeit wieder hergestellt werden:
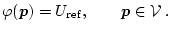 |
(3.41) |
Die folgende globale Verträglichkeitsbedingung muss immer erfüllt sein:
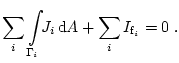 |
(3.42) |
Sie sagt aus, dass die Summe der Ströme über die
gesamte Leiteroberfläche gleich Null sein muss. Ist mindestens eine
Dirichlet-Bedingung vorhanden, so erfüllt die Lösung für das
Potenzial 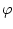 diese Bedingung automatisch, gibt es jedoch nur
Neumannsche und schwebende Randbedingungen, so muss (3.42) für den
Rand garantiert sein.
diese Bedingung automatisch, gibt es jedoch nur
Neumannsche und schwebende Randbedingungen, so muss (3.42) für den
Rand garantiert sein.
Aus den Gleichungen (3.7) und (3.9) kann die Stromdichte
bestimmt werden, (3.17) führt dann zu
Die Quellenfreiheit der Stromdichte ist gegeben durch
da der erste Term
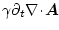 verschwindet (
verschwindet (
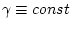 ), falls die Coulomb-Eichung gilt, ist
die Stromkontinuität sichergestellt, wenn der zweite Term ebenfalls
verschwindet.
), falls die Coulomb-Eichung gilt, ist
die Stromkontinuität sichergestellt, wenn der zweite Term ebenfalls
verschwindet.
Ein Satz von 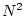 Induktivitäten ist definiert für ein System von N
Schleifen als
Induktivitäten ist definiert für ein System von N
Schleifen als
wobei 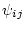 den magnetischen Fluß in der Schleife
den magnetischen Fluß in der Schleife 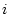 repräsentiert,
der auf den Strom
repräsentiert,
der auf den Strom 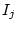 im Leiter
im Leiter 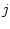 zurückzuführen ist. Anhand obiger
Definition könnte man die Induktivitäten ermitteln, aber der übliche Weg über die Berechnung der magnetischen Energie zeigt die
gleichen Resultate und ist überschaubarer, da die Berechnung der
Induktivitäten aus dem magnetischen Fluß mit größerem Aufwand verbunden ist. So läßt sich z.B. die Definition der
Integrationsflächen, die durch die Stromverteilungen gegeben sind, für ein
anspruchvolleres Beispiel nicht mehr einfach durchführen.
zurückzuführen ist. Anhand obiger
Definition könnte man die Induktivitäten ermitteln, aber der übliche Weg über die Berechnung der magnetischen Energie zeigt die
gleichen Resultate und ist überschaubarer, da die Berechnung der
Induktivitäten aus dem magnetischen Fluß mit größerem Aufwand verbunden ist. So läßt sich z.B. die Definition der
Integrationsflächen, die durch die Stromverteilungen gegeben sind, für ein
anspruchvolleres Beispiel nicht mehr einfach durchführen.
Die magnetische Energie ist zunächst gegeben durch das Integral, das über
den ganzen felderfüllten Raum ausgewertet werden muss
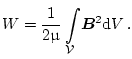 |
(3.46) |
Unter Verwendung von (3.8) und (3.11) ergibt sich
![$\displaystyle W=\frac{1}{2\protect{\mbox{{\usefont{U}{eur}{m}{n}\char22}}}}\int...
...\scriptstyle A$}} {\mbox{\boldmath$\scriptscriptstyle A$}})\big] \mathrm{d}V\,,$](img222.png) |
(3.47) |
und der Anwendung des Satzes von Gauß auf den zweiten Term
Gleichung (3.48) besteht aus einem Volumsintegral, das sich nur über
stromführende Gebiete erstreckt, und einem Oberflächenintegral, das für im
Endlichen gelegene Stromverteilungen verschwindet, wenn die Oberfläche gegen
unendlich geht. Dies läßt sich anhand einer Kugel
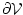 mit
Radius R veranschaulichen, die die ganze Stromverteilung einschließt, da die
Oberfläche nur proportional mit dem Quadrat des Radius wächst, während die
magnetische Feldstärke reziprok zur dritten Potenz des Radius und das
magnetische Vektorpotenzial reziprok zur zweiten Potenz des Radius abklingt.
Die magnetische Energie läßt sich mit (3.19) auch als doppeltes
Volumsintegral ausdrücken:
mit
Radius R veranschaulichen, die die ganze Stromverteilung einschließt, da die
Oberfläche nur proportional mit dem Quadrat des Radius wächst, während die
magnetische Feldstärke reziprok zur dritten Potenz des Radius und das
magnetische Vektorpotenzial reziprok zur zweiten Potenz des Radius abklingt.
Die magnetische Energie läßt sich mit (3.19) auch als doppeltes
Volumsintegral ausdrücken:
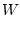 |
![$\displaystyle =\frac{\protect{\mbox{{\usefont{U}{eur}{m}{n}\char22}}}}{8\pi}\in...
...criptstyle r$}}'\vert} \mathrm{d}V \mathrm{d}V' =\frac{1}{2}\{I_i\}^T[L]\{I_j\}$](img226.png) |
(3.49) |
mit den Elementen 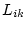 der Matrix [L]
der Matrix [L]
und der Spaltenmatrix der Schleifenströme 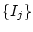 bzw. der transponierten
Spaltenmatrix
bzw. der transponierten
Spaltenmatrix 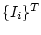 .
.
- Die Matrix ist symmetrisch, da (3.50) in
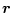 und
und
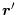 symmetrisch ist.
symmetrisch ist.
- Da die magnetische Energie für beliebige
Stromverteilungen stets positiv ist, ist
![$ [L]$](img234.png) positiv definit.
positiv definit.
- Es gibt keine Kopplung zwischen Leitern (Stromverteilungen), die
orthogonal zueinander sind.
- Die Kopplung ist negativ für Leiter, deren Stromverteilungen
antiparallele Richtungen aufweisen.
Diese Punkte decken sich mit den Aussagen von (1.3).
Fußnoten
- ...
Green-Funktionen3.1
- Im Zusammenhang mit Rand- und Anfangswertaufgaben
werden Grundlösungen auch Green-Funktionen genannt.
- ...
ist3.2
- Einfache Abschätzung der minimalen Wellenlänge für
Leitungssysteme mit maximaler Signalfrequenz von 4 GHz mittels
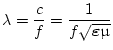 :
:
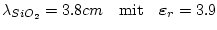
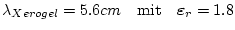
- ...
ermitteln3.3
- Ein ladungsbalanciertes System (
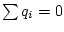 ) sei vorausgesetzt.
) sei vorausgesetzt.
C. Harlander: Numerische Berechnung von Induktivitšten in dreidimensionalen Verdrahtungsstrukturen
![]() gemäß der dritten Maxwellschen Gleichung (3.3).
Betrachtet man einen die Oberfläche eines Leiters umgebenden Bereich mit
der Dicke
gemäß der dritten Maxwellschen Gleichung (3.3).
Betrachtet man einen die Oberfläche eines Leiters umgebenden Bereich mit
der Dicke ![]() und lässt
und lässt ![]() gegen Null gehen, so erhält man die
Flächenladungsdichte
gegen Null gehen, so erhält man die
Flächenladungsdichte ![]() als Differenz der Normalkomponenten von
als Differenz der Normalkomponenten von
![]() außerhalb (
außerhalb (
![]() ) und innerhalb (
) und innerhalb (
![]() ) des
Leiters
) des
Leiters
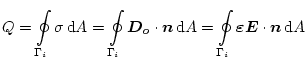
![]() lässt sich durch
lässt sich durch
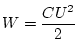
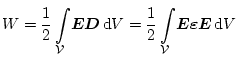
![]() erstreckt sich über das gesamte
Dielektrikum zwischen den Leitern und geht theoretisch i.a. bis ins
Unendliche. Das elektrische Feld ladungsbalancierter Leiter klingt für
Entfernungen, die groß gegenüber dem Durchmesser des Gebietes sind, das
die Ladungen enthält, mit der dritten Potenz des mittleren Abstands ab.
Deshalb ist der größte Teil der Feldenergie in der nächsten Umgebung
der Leiter enthalten und der Integrationsbereich kann für praktische
Anwendungen entsprechend verkleinert werden, ohne dass damit ein großer Fehler
bei der Energieberechnung gemacht wird.
erstreckt sich über das gesamte
Dielektrikum zwischen den Leitern und geht theoretisch i.a. bis ins
Unendliche. Das elektrische Feld ladungsbalancierter Leiter klingt für
Entfernungen, die groß gegenüber dem Durchmesser des Gebietes sind, das
die Ladungen enthält, mit der dritten Potenz des mittleren Abstands ab.
Deshalb ist der größte Teil der Feldenergie in der nächsten Umgebung
der Leiter enthalten und der Integrationsbereich kann für praktische
Anwendungen entsprechend verkleinert werden, ohne dass damit ein großer Fehler
bei der Energieberechnung gemacht wird.
![]() ) vorhanden sind, erhält man
die Euler-Gleichung
) vorhanden sind, erhält man
die Euler-Gleichung
![]() , auf dem Gleichung (3.27) gelöst werden soll, wird
durch mehrere Flächen berandet (Abb. 3.1).
, auf dem Gleichung (3.27) gelöst werden soll, wird
durch mehrere Flächen berandet (Abb. 3.1).

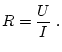
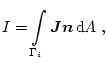
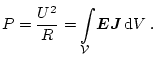
![]() Induktivitäten ist definiert für ein System von N
Schleifen als
Induktivitäten ist definiert für ein System von N
Schleifen als
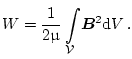
![$\displaystyle W=\frac{1}{2\protect{\mbox{{\usefont{U}{eur}{m}{n}\char22}}}}\int...
...\scriptstyle A$}} {\mbox{\boldmath$\scriptscriptstyle A$}})\big] \mathrm{d}V\,,$](img222.png)
![$\displaystyle =\frac{\protect{\mbox{{\usefont{U}{eur}{m}{n}\char22}}}}{8\pi}\in...
...criptstyle r$}}'\vert} \mathrm{d}V \mathrm{d}V' =\frac{1}{2}\{I_i\}^T[L]\{I_j\}$](img226.png)
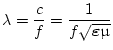 :
:
![]()
![]()