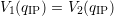 and either
and either 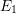 or
or
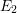 then specifies the classical barrier which has to be crossed. Assuming linear
coupling, i.e.
then specifies the classical barrier which has to be crossed. Assuming linear
coupling, i.e. 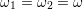 , yields
, yields
When there are no photons available for the transition, the process is called
non-radiative multi-phonon (NMP) process. Now the transition energy from one
parabolic minimum into the other has to be provided by phonons. Due
to energy conservation, a classical transition at the points is possible,
where the binding energy is zero. This is the case only at the intersection
point1
IP of (D.1) and (D.2). The value between 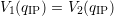 and either
and either 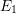 or
or
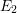 then specifies the classical barrier which has to be crossed. Assuming linear
coupling, i.e.
then specifies the classical barrier which has to be crossed. Assuming linear
coupling, i.e. 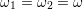 , yields
, yields
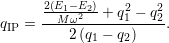 | (D.5) |
Reinserting (D.5) into (D.2) delivers
With the relaxation energy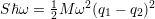 (cf. Fig. D.2), (D.6) can be
further evaluated to By combining (D.5) and (D.1),
(cf. Fig. D.2), (D.6) can be
further evaluated to By combining (D.5) and (D.1), 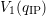 can be written as
can be written as
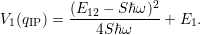 | (D.9) |
The forward and reverse rates then read
In Fig. D.2 all derived quantities are depicted. Again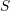 gives the number of
emitted phonons with an energy of
gives the number of
emitted phonons with an energy of 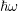 . Their product
. Their product 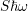 reflects the
strength of coupling and hence has a huge impact on the transition rates of the
defect states, e.g. a smaller
reflects the
strength of coupling and hence has a huge impact on the transition rates of the
defect states, e.g. a smaller 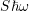 yields a smaller barrier.
yields a smaller barrier.
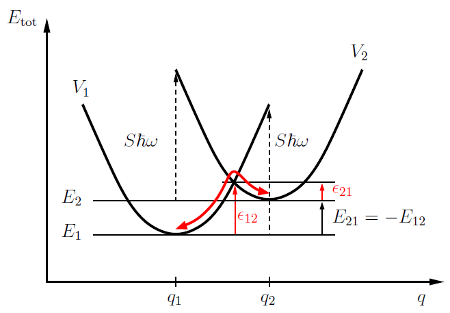
 in a reaction coordinate diagram
for the NMP model. The transition from one defect system into another
happens at the intersection of the energy curves. Usually one transition is
favored, inducing a preferred defect state. In this case the state
in a reaction coordinate diagram
for the NMP model. The transition from one defect system into another
happens at the intersection of the energy curves. Usually one transition is
favored, inducing a preferred defect state. In this case the state 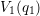 will
be occupied most of the time.
will
be occupied most of the time.