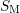 in Fig. 4.9 is bound between
in Fig. 4.9 is bound between 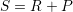 (the
extrapolated ‘true’ degradation) and
(the
extrapolated ‘true’ degradation) and 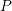 . The larger the delay time, the closer
. The larger the delay time, the closer
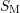 and
and 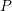 get and vice versa.
get and vice versa.
Based on the extracted model parameters of (4.5), a correlation between the
observed degradation and the measurement delay can be obtained. The actually
observable data marked with 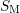 in Fig. 4.9 is bound between
in Fig. 4.9 is bound between 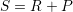 (the
extrapolated ‘true’ degradation) and
(the
extrapolated ‘true’ degradation) and 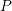 . The larger the delay time, the closer
. The larger the delay time, the closer
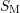 and
and 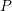 get and vice versa.
get and vice versa.
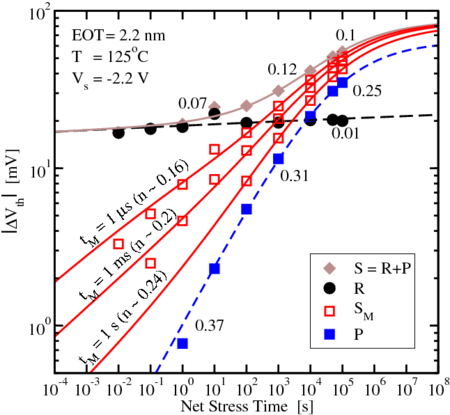
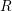 and
and 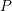 , lines:
model). The measurement results (
, lines:
model). The measurement results (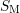 ) lie between
) lie between 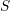 and
and 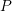 . Depending
on the measurement delay of the equipment (
. Depending
on the measurement delay of the equipment (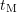 ) a broad range of ‘effective’
power-law slopes are observed (limiting values given next to the model lines).
) a broad range of ‘effective’
power-law slopes are observed (limiting values given next to the model lines).
When fitting the single stress sequences with varying 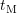 by a power-law,
different values of the slope are obtained which may be a reason why the
power-law exponents reported in NBTI literature vary that strongly. In
Fig. 4.10 the power-law slopes, defined as
by a power-law,
different values of the slope are obtained which may be a reason why the
power-law exponents reported in NBTI literature vary that strongly. In
Fig. 4.10 the power-law slopes, defined as 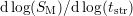 , are
shown. As can be seen the extrapolation with a power-law does not seem
to be the best choice to represent the time behavior of NBTI due to
the interplay between
, are
shown. As can be seen the extrapolation with a power-law does not seem
to be the best choice to represent the time behavior of NBTI due to
the interplay between 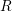 and
and 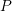 . Since the power-law extrapolation is
furthermore only approximately valid over a few decades in time, lifetime
prediction based on this approximate concept should be done with great
care.
. Since the power-law extrapolation is
furthermore only approximately valid over a few decades in time, lifetime
prediction based on this approximate concept should be done with great
care.

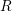 and
and 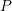 , lines:
model). The effective power-law slope as a function of the measurement
delay, defined as
, lines:
model). The effective power-law slope as a function of the measurement
delay, defined as 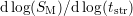 is only approximately valid over a
few decades in time within the standard measurement window. This is due
to the interaction between
is only approximately valid over a
few decades in time within the standard measurement window. This is due
to the interaction between 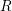 (depending on the measurement delay) and
(depending on the measurement delay) and
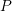 (indepenent of
(indepenent of 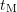 ).
).