 ,
, 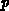 und
und 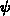




 ,
, 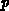 und
und 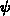
Die Darstellung der Formeln der Shockley-Read-Hall-Statistik
wird durch Verwendung einer zeitabhängigen Besetzungsfunktion
(Occupancy Function) 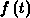 und einer weiteren Besetzungsfunktion im stationären Zustand,
und einer weiteren Besetzungsfunktion im stationären Zustand, 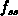 (Steady-State Occupancy Function) in folgender
Weise vereinfacht. Es gilt
(Steady-State Occupancy Function) in folgender
Weise vereinfacht. Es gilt
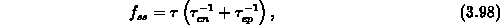
wobei die Zeitkonstante  durch
durch
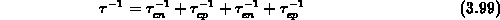
gegeben ist. Die zeitabhängige Störstellengleichung für die
Besetzungsfunktion 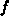 ist also die gewöhnliche Differentialgleichung
ist also die gewöhnliche Differentialgleichung
Daraus ist ersichtlich, daß im stationären Zustand
die Gleichheit 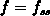 gilt,
da keine Änderung in der Besetzung erfolgt.
Zur Zeitkonstante
gilt,
da keine Änderung in der Besetzung erfolgt.
Zur Zeitkonstante  ist zu bemerken, daß jene
von den Ladungsträgerkonzentrationen
ist zu bemerken, daß jene
von den Ladungsträgerkonzentrationen  und
und 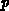 abhängig ist, weshalb
der Begriff Zeit-Konstante hier unangebracht ist, da diese
Größen zeitlich stark variieren können.
Die Raten für die Elektronen und Löcher
sind durch die Ausdrücke
abhängig ist, weshalb
der Begriff Zeit-Konstante hier unangebracht ist, da diese
Größen zeitlich stark variieren können.
Die Raten für die Elektronen und Löcher
sind durch die Ausdrücke
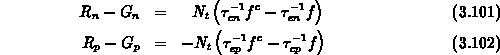
gegeben. Die Funktion 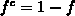 ist die zu
ist die zu 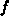 komplementäre Besetzungsfunktion.
Numerische Probleme resultieren aus der Tatsache, daß die
Fließkommazahlen der Computerarithmetik nicht gleichmäßig
auf der reellen Achse verteilt liegen. Insbesondere liegen
solche Zahlen um Null wesentlich dichter als um Eins. Die
Operation
komplementäre Besetzungsfunktion.
Numerische Probleme resultieren aus der Tatsache, daß die
Fließkommazahlen der Computerarithmetik nicht gleichmäßig
auf der reellen Achse verteilt liegen. Insbesondere liegen
solche Zahlen um Null wesentlich dichter als um Eins. Die
Operation 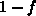 liefert mit
liefert mit 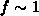 Werte, die
in der Größenordnung der Maschinengenauigkeit von
Werte, die
in der Größenordnung der Maschinengenauigkeit von 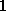 liegen, was bedeutet, daß der numerische Wert von
liegen, was bedeutet, daß der numerische Wert von 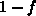 im Rundungsfehler verloren gegangen ist.
Dieser Fehler wird aber in Folge mit großen Zahlen
multipliziert, wodurch signifikante Fehler bei den Raten
entstehen. Ein Ausweg kann durch simultane
Berechnung von
im Rundungsfehler verloren gegangen ist.
Dieser Fehler wird aber in Folge mit großen Zahlen
multipliziert, wodurch signifikante Fehler bei den Raten
entstehen. Ein Ausweg kann durch simultane
Berechnung von 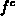 durch
durch
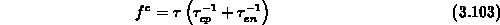
gefunden werden. Diese Funktion entsteht nicht
durch Subtraktion gleich großer Zahlen und ist
daher wesentlich genauer als die Maschinengenauigkeit von 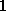 .
.
Neben der Besetzungsfunktion 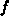 und ihrem Komplement
und ihrem Komplement
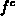 sind noch die Ableitungen nach den Halbleiter-Variablen
sind noch die Ableitungen nach den Halbleiter-Variablen
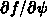 ,
, 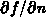 und
und
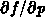 zu berechnen.
Dazu eine Vorbemerkung.
Es ist üblich, die Jacobi-Matrix
zu berechnen.
Dazu eine Vorbemerkung.
Es ist üblich, die Jacobi-Matrix 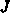 der Halbleitergleichungen
durch eine lineare Variablentransformation (Transformationsmatrix
der Halbleitergleichungen
durch eine lineare Variablentransformation (Transformationsmatrix 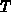 )
)
nach ,,führenden Termen`` zu diagonalisieren, wodurch die
Poissongleichung in der Jacobi-Matrix
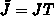 ,,regularisiert`` wird [4].
Weiters treten in der ersten Spalte von
,,regularisiert`` wird [4].
Weiters treten in der ersten Spalte von 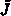 Subdiagonaleinträge auf, in denen die
Newton-Korrekturen im Divergenzoperator mit Stromdichten
multipliziert werden. Diese Matrixelemente sind
klein sobald die lokalen Stromdichten klein
sind. Der Operator
Subdiagonaleinträge auf, in denen die
Newton-Korrekturen im Divergenzoperator mit Stromdichten
multipliziert werden. Diese Matrixelemente sind
klein sobald die lokalen Stromdichten klein
sind. Der Operator 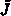 eignet sich deswegen
bei niederen Stromdichten gut zu einer entkoppelten Analyse,
da nur die Hauptdiagonalelemente eine signifikante
Rolle spielen.
eignet sich deswegen
bei niederen Stromdichten gut zu einer entkoppelten Analyse,
da nur die Hauptdiagonalelemente eine signifikante
Rolle spielen.
Im Hauptdiagonalelement in der ersten
Spalte der Jacobimatrix 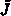 , dieses
entspricht der Poissongleichung im Gummel-Algorithmus,
tritt ein sogenannter Dämpfungsterm auf.
Dieser Term kann als Ableitung der Raumladung
nach dem elektrostatischen Potential im thermodynamischen
Gleichgewicht betrachtet werden.
Im Fall der Anwesenheit von Störstellen ist die
Abhängigkeit dieses Dämpfungsterms
vom Besetzungsgrad der Störstellen in der
Transformationsmatrix zu berücksichtigen.
Die Terme in der ersten Spalte der Transformationsmatrix
, dieses
entspricht der Poissongleichung im Gummel-Algorithmus,
tritt ein sogenannter Dämpfungsterm auf.
Dieser Term kann als Ableitung der Raumladung
nach dem elektrostatischen Potential im thermodynamischen
Gleichgewicht betrachtet werden.
Im Fall der Anwesenheit von Störstellen ist die
Abhängigkeit dieses Dämpfungsterms
vom Besetzungsgrad der Störstellen in der
Transformationsmatrix zu berücksichtigen.
Die Terme in der ersten Spalte der Transformationsmatrix 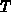 werden daher sinngemäß modifiziert:
werden daher sinngemäß modifiziert:
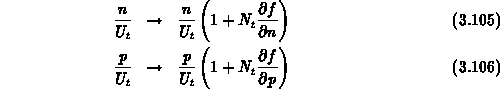
Im Gummel-Verfahren wird das nichtlineare Gleichungssystem
unter Vernachlässigung der Operatoren außerhalb der
Hauptdiagonale von 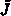 in der Reihenfolge
der Variablen
in der Reihenfolge
der Variablen 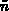 ,
, 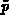 und
und 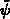 sequentiell gelöst,
was einem nichtlinearen Jacobi/Gauß-Seidel-Verfahren entspricht.
Die Form der regularisierten Poissongleichung
zeigt, daß pro Gummel-Schritt für die Poissongleichung
eine Newton-Korrektur für
sequentiell gelöst,
was einem nichtlinearen Jacobi/Gauß-Seidel-Verfahren entspricht.
Die Form der regularisierten Poissongleichung
zeigt, daß pro Gummel-Schritt für die Poissongleichung
eine Newton-Korrektur für 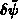 durchgeführt wird.
Für die Beiträge der Störstellen zur Dämpfungsfunktion
findet man im stationären Fall
durchgeführt wird.
Für die Beiträge der Störstellen zur Dämpfungsfunktion
findet man im stationären Fall
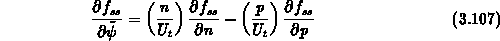
mit den Einzelableitungen
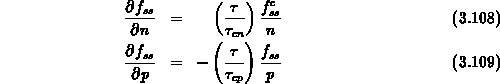
die Formel
Für den zeitabhängigen Fall wird die gewöhnliche
Differentialgleichung für 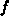 nach
nach 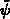 differenziert,
wodurch man unter Berücksichtigung des Satzes von Schwarz
die gewöhnliche Differentialgleichung
differenziert,
wodurch man unter Berücksichtigung des Satzes von Schwarz
die gewöhnliche Differentialgleichung
bezüglich der Zeit erhält.
Man sieht, daß die rechte Seite
von Gleichung (3.111)
ident ist mit der rechten Seite
von Gleichung (3.110), wenn die Funktion
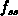 rein formal durch
rein formal durch 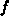 ersetzt wird. Von dieser
Eigenschaft läßt sich bei der Implementation vorteilhaft
Gebrauch machen.
ersetzt wird. Von dieser
Eigenschaft läßt sich bei der Implementation vorteilhaft
Gebrauch machen.
In analoger Vorgangsweise findet man für die
Ableitungen der Rekombinationsraten nach 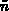 und
und 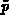
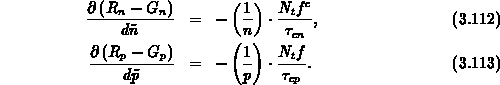
Es soll hier noch einmal darauf hingewiesen werden, daß
die Berücksichtigung der
Ableitungen von 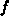 nach
nach  ,
, 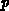 und insbesondere nach
und insbesondere nach
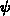 bei der nichtlinearen Gleichungslösung
wichtig, für hohe Störstellendichten
eine Voraussetzung ist.
Für hohe Störstellendichten, wie sie typisch bei
degradierten Transistoren der Fall sind, treten bei
Vernachlässigung dieser Ableitungen Oszillationen
im Gleichungslöser auf. In den meisten solchen Fällen
ist Konvergenz der nichtlinearen Iteration
nicht zu erreichen. Dies gilt sowohl
für den stationären als auch für den nichtstationären
Fall.
bei der nichtlinearen Gleichungslösung
wichtig, für hohe Störstellendichten
eine Voraussetzung ist.
Für hohe Störstellendichten, wie sie typisch bei
degradierten Transistoren der Fall sind, treten bei
Vernachlässigung dieser Ableitungen Oszillationen
im Gleichungslöser auf. In den meisten solchen Fällen
ist Konvergenz der nichtlinearen Iteration
nicht zu erreichen. Dies gilt sowohl
für den stationären als auch für den nichtstationären
Fall.



