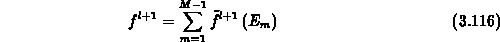3.9 Numerische Lösung und Implementation




Next: 3.10 Stationäre und nichtstationäre
Up: 3 Zeitveränderliche Generations- und
Previous: 3.8 Ableitungen nach
Während analytische Approximationen wie jene im
Abschnitt 3.5 zum grundlegenden
Verständnis der Dynamik solcher Prozesse unerläßlich
sind, erlaubt die numerische Lösung des Gesamtsystems
von Gleichungen quantitative Aussagen für Fälle,
in denen die analytischen Formeln aufgrund ihrer
einschränkenden Voraussetzungen ihre Gültigkeit
verlieren. Andererseits aber erlaubt die Simulation,
jene Schranken zu bestimmen, in denen die analytischen
Formeln erst gültig werden. Eine solche Schranke ist
z.B. der Übergangspunkt von der stationären
zur nichtstationären Grenzflächen-Emission.
Die erstere ist von der Lage des
Quasi-Ferminiveaus an der Grenzfläche abhängig,
die letztere nicht.
Sie kann durch analytische Formeln quantitativ sehr
gut erfaßt werden, was große praktische Bedeutung
hat.
Die zeitabhängige Bilanzgleichung einer
Störstelle des Energieniveaus 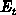 ist eine gewöhnliche, lineare
Differentialgleichung der Variablen
ist eine gewöhnliche, lineare
Differentialgleichung der Variablen 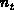 .
Die Koeffizienten dieser Gleichung sind jedoch sowohl
orts- als auch zeitabhängig und können
sowohl örtlich als auch zeitlich stark variieren.
Anfangsrandwertprobleme dieses Typs werden als ,,steif``
bezeichnet und erfordern in der Regel
eine implizite Zeit-Diskretisierung, um Instabilitäten
hinsichtlich der Zeit zu vermeiden.
Das einfachste
Verfahren ist von erster Ordnung (Rückwärts-Euler-Verfahren).
Zur Diskretisierung denke man
sich die Zeit durch ein nicht äquidistantes
Gitter
.
Die Koeffizienten dieser Gleichung sind jedoch sowohl
orts- als auch zeitabhängig und können
sowohl örtlich als auch zeitlich stark variieren.
Anfangsrandwertprobleme dieses Typs werden als ,,steif``
bezeichnet und erfordern in der Regel
eine implizite Zeit-Diskretisierung, um Instabilitäten
hinsichtlich der Zeit zu vermeiden.
Das einfachste
Verfahren ist von erster Ordnung (Rückwärts-Euler-Verfahren).
Zur Diskretisierung denke man
sich die Zeit durch ein nicht äquidistantes
Gitter 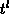 ,
, 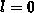 ,
, 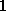 ,
,  ,
,  mit
den Gitterabständen
mit
den Gitterabständen 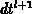 =
=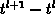 ,
, 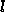 =
=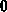 ,
,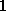 ,
, ,
, ,
diskretisiert.
Die implizite diskrete Version von
Gleichung (3.100) lautet
,
diskretisiert.
Die implizite diskrete Version von
Gleichung (3.100) lautet
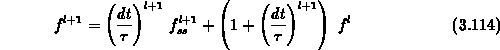
und analog dazu die Gleichung (3.111) für die
Ableitung nach dem Potential 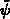
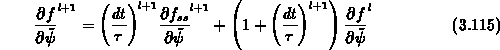
falls, wie im vorangegangenen Abschnitt bemerkt,
die Funktion 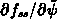 mit
dem Argument
mit
dem Argument 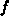 anstatt von
anstatt von 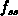 benutzt wird.
Löst man aus numerischen Gründen auch die komplementäre
Besetzungsfunktion
benutzt wird.
Löst man aus numerischen Gründen auch die komplementäre
Besetzungsfunktion 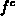 nach der Zeit, so ist
auch dafür eine gewöhnliche Differentialgleichung
analog zu (3.114) mitzuführen.
nach der Zeit, so ist
auch dafür eine gewöhnliche Differentialgleichung
analog zu (3.114) mitzuführen.
Diese Gleichungen wurden in das Simulationsprogramm MINIMOS
implementiert.
Grundsätzlich werden donator- und akzeptorartige Störstellen
gemeinsam zugelassen, jedoch getrennt berechnet.
Es existieren
Bilanzgleichungen für beide Störstellentypen,
wobei nach erfolgter Lösung dieser Gleichungen
die Raten und die resultierenden Ladungen überlagert werden.
Die Ableitungen nach  ,
, 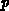 werden vor der Lösung der
Kontinuitätsgleichungen, die Ableitungen nach
werden vor der Lösung der
Kontinuitätsgleichungen, die Ableitungen nach 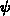 vor der Lösung der Poissongleichung bzw. der zeitdifferenzierten
Poissongleichung berechnet.
vor der Lösung der Poissongleichung bzw. der zeitdifferenzierten
Poissongleichung berechnet.
Die Gleichungen (3.114) bzw. (3.115)
gelten in dieser Form für diskrete Volumenstörstellen,
wobei deren räumliche Verteilung als homogen angenommen wird.
Diese diskreten Störstellen sind
wichtig zur transienten Analyse von Galliumarsenid MESFETs,
deren Simulation mit MINIMOS ebenfalls
möglich ist [48][60][61].
Aufgrund der Verteilung der Grenzflächen-Störstellen
in der Energielücke einerseits und der räumlichen
Verteilung an der 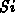 -
-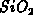 Grenzfläche andererseits
sind zur realistischen Simulation verteilter Störstellen
einige Parameter vorzugeben. Die folgende Liste
gibt einen Überblick über die
möglichen Eingaben in MINIMOS:
Grenzfläche andererseits
sind zur realistischen Simulation verteilter Störstellen
einige Parameter vorzugeben. Die folgende Liste
gibt einen Überblick über die
möglichen Eingaben in MINIMOS:
- -
- Einfangquerschnitte
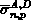 für Elektronen und Löcher, sowohl für donator- und akzeptorartige
Störstellen. Diese sind räumlich und energetisch uniform.
für Elektronen und Löcher, sowohl für donator- und akzeptorartige
Störstellen. Diese sind räumlich und energetisch uniform.
- -
-
Störstellenverteilungen an der (den)
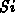 -
-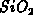 Grenzfläche(n).
Sowohl räumlich uniforme als auch lokalisierte, normalverteilte
Störstellenverteilungen sind möglich.
Grenzfläche(n).
Sowohl räumlich uniforme als auch lokalisierte, normalverteilte
Störstellenverteilungen sind möglich.
- -
-
Störstellenverteilungen im verbotenen Band. Uniforme
und lineare Verteilungen sind möglich.
Spezifikation von Störstellenparametern an der rückwärtigen
Grenzfläche von Dünnfilm SOI-MOSFETs werden im
Abschnitt 4.2 behandelt.
Zur numerischen Berechnung verteilter
Störstellen wird eine äquidistante Diskretisierung
der Generations- und Rekombinationsraten bzw. der
zeitabhängigen Besetzungsfunktion im Bereich des
verbotenen Bandes durchgeführt, wobei der Gitterabstand
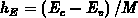 durch den Parameter
durch den Parameter 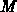 (
(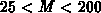 ) vorgebbar ist.
Die totalen, energieunabhängigen
Generations- und Rekombinationsraten für donator-
bzw. akzeptorartige verteilte Störstellen ergeben
sich gemäß dem diskretisierten Äquivalent der
Gleichungen (3.54)-(3.56)
durch Summation über das gesamte verbotene Band.
Gleichermaßen ist die totale Besetzungsfunktion
durch
) vorgebbar ist.
Die totalen, energieunabhängigen
Generations- und Rekombinationsraten für donator-
bzw. akzeptorartige verteilte Störstellen ergeben
sich gemäß dem diskretisierten Äquivalent der
Gleichungen (3.54)-(3.56)
durch Summation über das gesamte verbotene Band.
Gleichermaßen ist die totale Besetzungsfunktion
durch
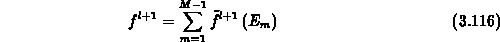
gegeben und die Ableitung nach dem elektrostatischen
Potential durch





Next: 3.10 Stationäre und nichtstationäre
Up: 3 Zeitveränderliche Generations- und
Previous: 3.8 Ableitungen nach
Martin Stiftinger
Fri Oct 14 21:33:54 MET 1994
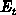 ist eine gewöhnliche, lineare
Differentialgleichung der Variablen
ist eine gewöhnliche, lineare
Differentialgleichung der Variablen 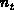 .
Die Koeffizienten dieser Gleichung sind jedoch sowohl
orts- als auch zeitabhängig und können
sowohl örtlich als auch zeitlich stark variieren.
Anfangsrandwertprobleme dieses Typs werden als ,,steif``
bezeichnet und erfordern in der Regel
eine implizite Zeit-Diskretisierung, um Instabilitäten
hinsichtlich der Zeit zu vermeiden.
Das einfachste
Verfahren ist von erster Ordnung (Rückwärts-Euler-Verfahren).
Zur Diskretisierung denke man
sich die Zeit durch ein nicht äquidistantes
Gitter
.
Die Koeffizienten dieser Gleichung sind jedoch sowohl
orts- als auch zeitabhängig und können
sowohl örtlich als auch zeitlich stark variieren.
Anfangsrandwertprobleme dieses Typs werden als ,,steif``
bezeichnet und erfordern in der Regel
eine implizite Zeit-Diskretisierung, um Instabilitäten
hinsichtlich der Zeit zu vermeiden.
Das einfachste
Verfahren ist von erster Ordnung (Rückwärts-Euler-Verfahren).
Zur Diskretisierung denke man
sich die Zeit durch ein nicht äquidistantes
Gitter 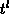 ,
, 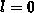 ,
, 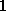 ,
,  ,
,  mit
den Gitterabständen
mit
den Gitterabständen 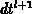 =
=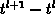 ,
, 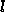 =
=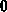 ,
,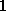 ,
, ,
, ,
diskretisiert.
Die implizite diskrete Version von
Gleichung (3.100) lautet
,
diskretisiert.
Die implizite diskrete Version von
Gleichung (3.100) lautet




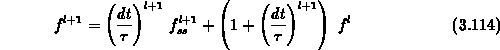
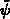
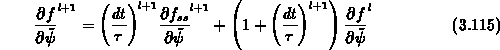
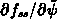 mit
dem Argument
mit
dem Argument 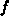 anstatt von
anstatt von 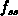 benutzt wird.
Löst man aus numerischen Gründen auch die komplementäre
Besetzungsfunktion
benutzt wird.
Löst man aus numerischen Gründen auch die komplementäre
Besetzungsfunktion 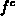 nach der Zeit, so ist
auch dafür eine gewöhnliche Differentialgleichung
analog zu (
nach der Zeit, so ist
auch dafür eine gewöhnliche Differentialgleichung
analog zu ( ,
, 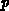 werden vor der Lösung der
Kontinuitätsgleichungen, die Ableitungen nach
werden vor der Lösung der
Kontinuitätsgleichungen, die Ableitungen nach 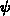 vor der Lösung der Poissongleichung bzw. der zeitdifferenzierten
Poissongleichung berechnet.
vor der Lösung der Poissongleichung bzw. der zeitdifferenzierten
Poissongleichung berechnet.
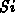 -
-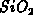 Grenzfläche andererseits
sind zur realistischen Simulation verteilter Störstellen
einige Parameter vorzugeben. Die folgende Liste
gibt einen Überblick über die
möglichen Eingaben in MINIMOS:
Grenzfläche andererseits
sind zur realistischen Simulation verteilter Störstellen
einige Parameter vorzugeben. Die folgende Liste
gibt einen Überblick über die
möglichen Eingaben in MINIMOS:
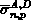 für Elektronen und Löcher, sowohl für donator- und akzeptorartige
Störstellen. Diese sind räumlich und energetisch uniform.
für Elektronen und Löcher, sowohl für donator- und akzeptorartige
Störstellen. Diese sind räumlich und energetisch uniform.
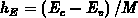 durch den Parameter
durch den Parameter 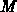 (
(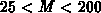 ) vorgebbar ist.
Die totalen, energieunabhängigen
Generations- und Rekombinationsraten für donator-
bzw. akzeptorartige verteilte Störstellen ergeben
sich gemäß dem diskretisierten Äquivalent der
Gleichungen (3.54)-(3.56)
durch Summation über das gesamte verbotene Band.
Gleichermaßen ist die totale Besetzungsfunktion
durch
) vorgebbar ist.
Die totalen, energieunabhängigen
Generations- und Rekombinationsraten für donator-
bzw. akzeptorartige verteilte Störstellen ergeben
sich gemäß dem diskretisierten Äquivalent der
Gleichungen (3.54)-(3.56)
durch Summation über das gesamte verbotene Band.
Gleichermaßen ist die totale Besetzungsfunktion
durch