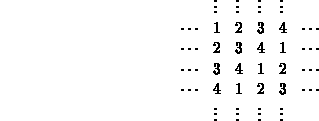
,,There seems to be an incompatibility between parallelism and good
orderings for ICCG.``
Iain Duff et al. [20]
Poole und Ortega [84] zeigten, wie sich unvollständige Faktorisierungen durch Umsortierung der Unbekannten parallelisieren lassen. Die Idee ist einfach: Im Falle eines Tensor-Produkt-Gitters werden die Unbekannten mit p ,,Farben`` zyklisch numeriert. Ein Beispiel mit vier Farben in zwei Dimensionen ist
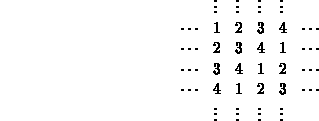
Sortiert man die Unbekannten gleicher Farbe in der Koeffizientenmatrix, so erhält die neue Matrix eine Block-Struktur mit p Blöcken:
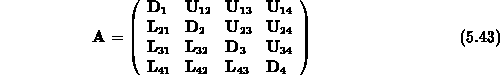
Die Matrix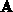 
läßt sich blockweise ILU-faktorisieren,
wobei rekursiv für die diagonalen Blöcke mit 
=
,
,
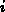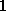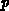die Gleichung
gelöst werden muß. Wie bei der punktweisen ILU-Faktorisierung
sind die Matrizen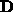 
, 
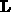und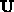 
durch das
Spärlichkeitsmuster der umsortierten Matrix festgelegt
Die Vorkonditionierungsmatrix hat die Gestalt (MC bedeutet Multi-Color)
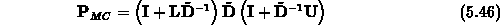
und die Faktorisierungsgleichung (5.44) resultiert aus der Forderung
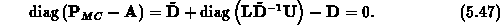
Die Variablen innerhalb der Blöcke sind voneinander
unabhängig, demgemäß ist die Vektorlänge durch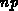 
gegeben,
wobei 
die Anzahl der Unbekannten ist.
Eine maximale Vektorlänge von
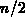ergibt sich für zwei Farben. Dies entspricht gerade
einer Schachbrettnumerierung (zwei Farben)
oder einer Rot-Schwarz-Einfärbung (Red-Black-Ordering).
Die Matrix-Struktur ist
bei einer Partitionierung in rote (R) und schwarze (B)
Punkte
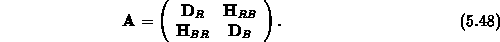
Nach der Elimination der schwarzen Punkte erhält man das sogenannte reduzierte System
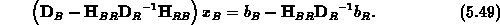
Die Diagonalmatrix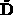 
ergibt sich
gemäß Gleichung (5.44) zu
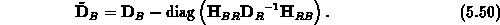
Das reduzierte System wird mit 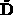symmetrisch
skaliert
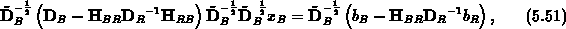
was schließlich nach der Variablentransformation
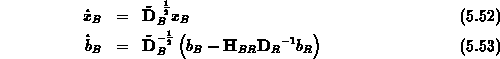
das vorkonditionierte System
ergibt. Die Berechnung des vorkonditionierten Matrix-Vektor-Produktes umfaßt die beiden Schritte
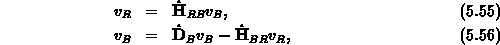
wobei beim ersten Schritt Daten über die Matrix
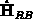von den schwarzen zu den
roten Punkten abgebildet, beim zweiten Schritt
Daten von den roten zu den schwarzen Punkten
über die Matrix 
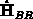zurücktransportiert werden.
Nach Abbruch der Iteration muß die Lösung
für die roten Punkte aus der Lösung der schwarzen Punkte
mit der Formel
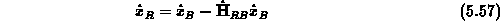
rücksubstituiert werden. Es soll hinzugefügt werden,
daß diagonale Skalierung des reduzierten
Systems einerseits und ILU-Faktorisierung nach RB-Umsortierung
andererseits identische Methoden sind.
Die Konvergenz des Gleichungslösers wird durch die
Umsortierung stark beeinflußt. Untersuchungen
dieses Typs für das CG-Verfahren wurden in [20] vorgenommen.
Die heuristische Schlußfolgerung
der Autoren ist, daß die einfache
lexikographische (natürliche) Ordnung
der Unbekannten gute Konvergenzeigenschaften, entkoppelte
Ordnungs-Verfahren wie z.B. das Multicolor-Ordnungs-Verfahren
schlechte Konvergenzeigenschaften des
ICCG-Algorithmus nach sich ziehen. Die Unterschiede sind
umso drastischer, je schlechter konditioniert
das Problem ist. Generell gute Ordnungs-Verfahren
sind solche, die lokal sind, was
bedeutet, daß die Numerierung der Unbekannten
so zu erfolgen hat, daß benachbarte Knoten
,,nahe`` beisammen zu liegen kommen.
