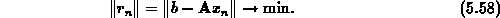
Die Idee, Matrix-Polynome der Koeffizientenmatrix
als Vorkonditionierung zu benutzen,
ist naheliegend, da Matrizenpolynome insbesondere
auf parallelen Systemen und bei
Vorliegen von Tensor-Produkt-Gittern leicht
zu evaluieren sind. Die Auswertegeschwindigkeit
eines Matrizenpolynoms ist in erster Linie
von der Matrix-Vektor-Multiplikationsroutine abhängig.
Die ersten Vorschläge zur polynomialen
Vorkonditionierung wurden durch das Erscheinen
der ersten Vektorcomputer motiviert [19].
Da die unvollständigen Cholesky-Faktoren
im ICCG-Algorithmus nicht gut vektorisierten,
behalf man sich durch Reihenentwicklungen
der unvollständigen LU-Faktoren in Neumann-Polynome.
In ähnlicher Weise wurde in [1]
eine sogenannte m-step-Jacobi-Vorkonditionierung
vorgeschlagen. Es ist leicht zu sehen,
daß nur Polynome mit ungeradem Grad sinnvoll sind.
Für schlecht konditionierte Probleme liefern
diese Reihenentwicklungen aber wesentlich
schlechtere Konvergenzresultate als die originale
unvollständige Faktorisierung. Bei solchen
Problemen wird der Vektorisierungsgewinn
der polynomialen Vorkonditionierung durch
die Konvergenz-Degradation verloren.
Eine besondere Situation ist bei massiv-parallelen
SIMD-Architekturen gegeben.
Solche Systeme verfügen über ein
Datenkommunikationsnetzwerk, das Datentransport
zwischen Nachbarprozessoren begünstigt.
Die Rücksubstitution der unvollständigen
Faktoren parallelisiert auf einem solchen
System besonders schlecht. Ein zweiter
,,Flaschenhals`` im Berechnungsfluß ist
die Berechnung innerer Produkte im
CG-Verfahren in den verwandten Verfahren
für nichtsymmetrische Probleme,
die eine globale Kommunikation der Prozessoren erfordert.
Die Unattraktivität globaler Kommunikation
wirft ein Licht auf Verfahren, die ein
Mindestmaß einer solchen benötigen.
Solche Algorithmen sind z.B. polynomial-vorkonditionierte
iterative Verfahren.
Eine allgemeine Betrachtung polynomialer
Vorkonditionierung wurde in [51]
vorgenommen. Die grundlegende Idee ist die
folgende: Die Lösung eines
linearen Gleichungssystems ist äquivalent
mit der Minimierung einer geeigneten
Norm des Residuenvektors
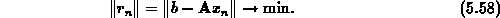
Konstruiert man ein Matrix-Polynom
des Grades 
für den Lösungsvektor
, so findet man
für das Residuum die Polynomdarstellung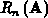 
wenn als Startvektor der polynomialen Iteration die
rechte Seite des Gleichungssystems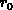 
=
,
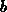d.h.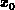 
=
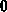gewählt wird.
Das Residuenpolynom hat die
wichtige Eigenschaft
Zur Bestimmung der Polynomkoeffizienten von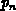 
muß eine
Extremwertaufgabe für das Residuenpolynom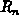 
gelöst werden:
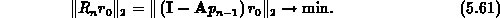
Dieses Minimierungsproblem für Matrizen
kann nach Entwicklung von 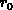im
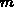-dimensionalen Eigenraum des positiv-definiten Operators
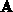spektral gelöst werden
(
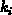sind die Eigenkomponenten von ):
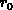Die Lösung dieses Problems führt auf eine Variante des CG-Algorithmus, den sogenannten CR-Algorithmus (Conjugate Residual Algorithm) [105]. Das auf der diskreten Wichtung der Eigenkomponenten aufbauende Kriterium (5.62) kann unter Einführung der Dichtefunktion
in die integrale Darstellung
übergeführt werden.
Für eine allgemeine positive
Funktion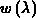 
nennt man diese
Aufgabe das spektrale Fitting-Problem.
Die Lösung eines solchen Optimierungsproblems
sind normierte
Kern-Polynome
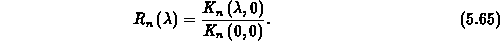
Es ist einfach zu zeigen, daß die Polynome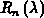 
orthogonal bezüglich der Gewichtsfunktion 
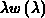sind [105].
Diese wichtige Eigenschaft kann man mit einer geeigneten
Wahl der Gewichtsfunktionen 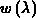verbinden,
um einfache rekursive Formeln für die
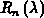herzuleiten.
Die Lage der extremalen
Eigenwerte 
,
,
die die Integrationsgrenzen in (5.64) definieren,
ist nicht bekannt. Am einfachsten
approximiert man mit .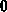
Einen Schätzwert für bekommt man aus dem
Gerschgorin-Theorem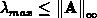 
.
Wählt man als Gewicht 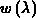die Funktion
(
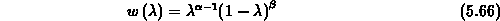
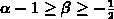), so ist
zu sehen, daß die 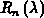orthogonal
bezüglich der Gewichtsfunktion
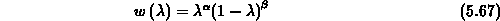
sind. Die orthogonalen Polynome sind die Jacobi-Polynome
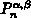, die auf dem Intervall [
,
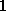] orthogonal
sind. Als Residuenpolynome erhält man nach Verschiebung und
Skalierung der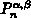 
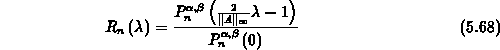
gegeben. Das Vorkonditionierungspolynom wird aus der Formel
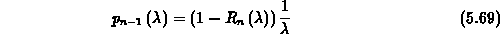
gewonnen. Mit der Beziehung
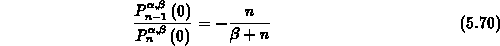
findet man eine Dreitermrekursion für die Evaluierung des Vorkonditionierungspolynoms
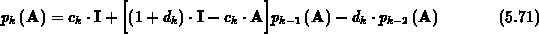
mit dem Parametersatz
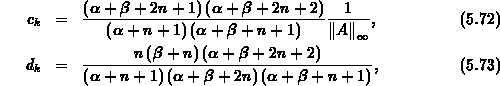
und den Anfangsvektoren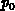 
=
=.
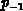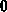Es besteht Freiheit in der Wahl der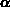 
und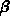 
.
=
,
=
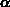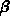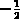führt auf Tschebyscheff-Polynome erster Art für die Residuen.
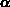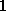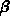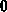=, = führt auf Legendresche Polynome.
Die erste Variante wurde als polynomiale Vorkonditionierung
in [89] untersucht, die letztere in [51].
In dieser Arbeit
wurden ausschließlich Legendresche Polynome verwendet.
Numerische Experimente werden im folgenden Abschnitt beschrieben.
