- (T1)
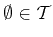 and
and
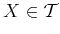 .
.
- (T2) a finite intersection of members of
 is in
is in
 .
.
- (T3) an arbitrary union of members of
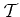 is in
is in
 .
.
To model space and time within the regime of a finite computer representation, the continuous domain has to be projected onto finite domains or cells. This chapter describes how these cells can be introduced and manipulated algebraically1.1, and is mainly based on the work of Jänich [2] for common topological terms, Berti [18] for the cell complexes, and Zomorodian [19] for the computational topology part. The most basic property of topology is that it separates global space properties from local geometric attributes. Additionally, and more importantly for this work, it provides a precise notation and language for discussing and handling various properties.
Topological spaces offer several operations for sets and subsets. The formal definition of a topological space is given next, where only the concept of a set is implied:
The second property (T2) states that arbitrary intersections of
subsets have to be in the topological space again. Also the union (T3)
of subsets has to be contained in the space. These properties are
later used to describe inter-dimensional elements for the complex,
such as edges of a cell. An example is given in the following which
presents a basic set
![]() and the corresponding
topology. This pair of the original set and the set of subsets
generates the topological space. Vertices are modeled by the
singletons
and the corresponding
topology. This pair of the original set and the set of subsets
generates the topological space. Vertices are modeled by the
singletons ![]() ,
, ![]() , and
, and ![]() .
.
| (1.23) |
To introduce the concept of a topological base, it is necessary to
create a topology on a set
![]() in which a set
in which a set
![]() of
subsets of
of
subsets of
![]() are open sets.
are open sets.
With these definitions, sets of subsets can be handled with additional
properties in a common way. The common definition for a topological
space is very general and allows several topological spaces which are
not useful in the field of data structures, e.g., a topological space
![]() with a trivial topology
with a trivial topology
![]() . Therefore the basic mechanism of separation
within a topological space is introduced.
Of a hierarchy of possible separation conditions augmenting the
topological space axioms, an important characteristic is the
Hausdorff condition.
. Therefore the basic mechanism of separation
within a topological space is introduced.
Of a hierarchy of possible separation conditions augmenting the
topological space axioms, an important characteristic is the
Hausdorff condition.
Common data structures in the field of scientific computing embody the separation characteristics of a Hausdorff space. The assumption to be made is that all scientific data can be modeled by the concept of a Hausdorff space. This can be seen as a generalization of Butler's model, which is based on the assumption that all scientific data can be modeled by trivial fiber bundles [21].
The concept of a cover is introduced to equip a topological space with a type of dimension.
If a topological space is homeomorphic to
![]() with
with
![]() , then its dimension is
, then its dimension is ![]() . If a space does not have a Lebesgue
covering dimension
. If a space does not have a Lebesgue
covering dimension ![]() for any
for any
![]() , it is called
infinite-dimensional. The dimension of the empty set
, it is called
infinite-dimensional. The dimension of the empty set ![]() is
defined as
is
defined as ![]() .
It is important to note that the reverse it not always true, which
means that a topological space with dimension
.
It is important to note that the reverse it not always true, which
means that a topological space with dimension ![]() is not necessarily
homeomorphic to
is not necessarily
homeomorphic to
![]() .
.
Another fundamental topological concept is compactness, which may be regarded as a substitute for finiteness. It frequently compensates for the restriction to finite intersections in axiom (T2) by allowing arbitrary sets of open sets to be reduced to finite sets of sets.
An important part of the characterization of data structures is the possibility to identify the object with the highest dimension, modeled by the concept of an open cell.
Collections of cells form larger structures, so-called complexes which
are identified by the cell with the highest dimension, e.g., a
![]() -dimensional space contains
-dimensional space contains ![]() -cells.
-cells.
With the concepts already introduced, the concept of a cell complex can be formulated.
Definition: CW-Complex
![]() [2]
[2]
A pair
![]() , with
, with ![]() a Hausdorff space and a
decomposition
a Hausdorff space and a
decomposition ![]() into cells is called a CW-Complex if and only
if the following axioms are satisfied:
into cells is called a CW-Complex if and only
if the following axioms are satisfied:
A CW-cell complex with the underlying space
![]() guarantees that
all inter-dimensional objects are connected in an appropriate manner,
such that
guarantees that
all inter-dimensional objects are connected in an appropriate manner,
such that ![]() is obtained from
is obtained from ![]() by attaching
by attaching
![]() -cells to each
-cells to each ![]() -cell and
-cell and
![]() . The
respective subspaces
. The
respective subspaces ![]() are called the
are called the ![]() -skeletons of the
cell complex.
-skeletons of the
cell complex.
A ![]() -cell describes the cell with the highest dimension, e.g.,
-cell describes the cell with the highest dimension, e.g.,
![]() -cell edges and
-cell edges and ![]() -cell triangles.
For this work the most important property of a CW-complex can be
explained by using different
-cell triangles.
For this work the most important property of a CW-complex can be
explained by using different ![]() -cells and consistently attaching
sub-dimensional cells to the
-cells and consistently attaching
sub-dimensional cells to the ![]() -cells. This fact is taken care of by
the mapping function.
For the common case a
-cells. This fact is taken care of by
the mapping function.
For the common case a ![]() -cell can be described by the oriented
collection of the 0
-cells, e.g., for a simplex cell
-cell can be described by the oriented
collection of the 0
-cells, e.g., for a simplex cell
![]() , which is introduced in more detail in Section
1.3.1.
, which is introduced in more detail in Section
1.3.1.
So far all mechanisms to handle the underlying topological space of data structures have been introduced. Each subspace can be uniquely characterized by its dimension. All subspaces are connected appropriately by the concept of a finite CW-cell complex.
The following section introduces concepts of order theory to formalize the combinatorial structure of cells and the global structure of cell complexes [54]. First, the most basic notion of a binary relation is introduced which is a specialization of the relation concept, where two arguments are used.
 |
|
Figure 1.2:
Left: Integers form a chain, totally ordered by |
Finally, the concept of covering is needed. For ![]() ordered by
ordered by ![]() , it is said
, it is said ![]() is covered by
is covered by ![]() (written
(written ![]() ), if
), if ![]() and for any
and for any ![]() ,
,
![]() implies
implies ![]() . This means that there is no element of
. This means that there is no element of ![]() "between"
"between" ![]() and
and
![]() . Equivalently it can be said that
. Equivalently it can be said that ![]() covers
covers ![]() .
.
It can be seen that in interpreting diagrams, it does not matter
whether one node is above or below another unless there is a monotonic
path between them; and that if there is a monotonic path from ![]() through one or more nodes down to
through one or more nodes down to ![]() , there is no separate edge
directly from
, there is no separate edge
directly from ![]() to
to ![]() , as can be seen in Figure 1.2.
, as can be seen in Figure 1.2.
The ![]() of two elements
of two elements ![]() corresponds to their geometric
intersection
corresponds to their geometric
intersection
![]() , the
, the ![]() to the element
to the element ![]() of
least dimension containing both of them
of
least dimension containing both of them
![]() . The
. The ![]() of two elements may be the whole mesh.
The poset of a convex polytope is an atomic and coatomic
lattice.
For an arbitrary complex, the poset is in general not a lattice. If a
grid's lattice is atomic, it means that
of two elements may be the whole mesh.
The poset of a convex polytope is an atomic and coatomic
lattice.
For an arbitrary complex, the poset is in general not a lattice. If a
grid's lattice is atomic, it means that ![]() -cells are uniquely
determined by their vertex sets if the lattice is coatomic, the
vertex sets of
-cells are uniquely
determined by their vertex sets if the lattice is coatomic, the
vertex sets of ![]() -cells for
-cells for ![]() can be determined from the
knowledge of the vertex sets of the
can be determined from the
knowledge of the vertex sets of the ![]() -cells alone.
-cells alone.
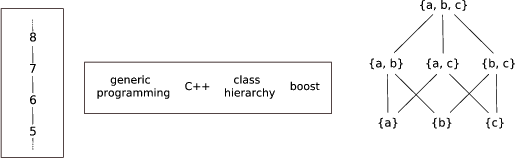
Order concepts for sets just introduced can be used to formalize the
internal structure of an arbitrary ![]() -cell, e.g., with the Hasse
diagram. A simplex cell is thereby distinguishable from a cuboid cell
type in several dimensions as depicted in Figure
1.3 and Figure
1.4, respectively.
-cell, e.g., with the Hasse
diagram. A simplex cell is thereby distinguishable from a cuboid cell
type in several dimensions as depicted in Figure
1.3 and Figure
1.4, respectively.
Also, sub-cells such as the corresponding edges and facets and their
direct relations to the cell can be identified.
An example of extracting all edges of the simplex cell which
corresponds with the middle layer of the Hasse diagram can also be
seen in Figure 1.3.
Another important fact to mention is that the topological structure
and the corresponding order hierarchy is invariant of the type of cell
used. The ![]() -layer of the cuboid cell represents the edges of this
type of cell.
-layer of the cuboid cell represents the edges of this
type of cell.
As a higher dimensional example, a three-dimensional simplex example is given in Figure 1.5.
Here, the ![]() -cells are the facets, and, in this particular example,
triangles. By using the actual dimension of the
-cells are the facets, and, in this particular example,
triangles. By using the actual dimension of the ![]() -cell and deriving
the
-cell and deriving
the ![]() cells only by means of the order structure, a flexible
framework can be built, where an important property for characterizing
cell complexes is required, the regularity of cells and the
complex. If the mapping function
cells only by means of the order structure, a flexible
framework can be built, where an important property for characterizing
cell complexes is required, the regularity of cells and the
complex. If the mapping function ![]() extends to a homeomorphism
on the whole of
extends to a homeomorphism
on the whole of
![]() , then the
, then the ![]() -cell is regular; its
sides are then homeomorphic to a decomposition of
-cell is regular; its
sides are then homeomorphic to a decomposition of
![]() ,
the boundary. The cell complex
,
the boundary. The cell complex
![]() is regular if all
cells are regular. The lattice property of a cell complex then
guarantees that intersections of the vertex sets of elements always
uniquely define a lower dimensional element.
is regular if all
cells are regular. The lattice property of a cell complex then
guarantees that intersections of the vertex sets of elements always
uniquely define a lower dimensional element.
In contrast to the internal cell topology, a cell complex requires adjacence information of cells. There are different possibilities of storing this information efficiently [35,53]. This work develops an abstract means of storing all different types of cells orthogonally, based on the cell topology of the complex topology. For dimensions greater than one, Figure 1.6 illustrates the complex topology of a 2-simplex cell complex where the bottom sets are now the cells. The rectangle in the figure marks the relevant cell number.
The topology of the cell complex is only available locally because of the fact that the top set can have an arbitrary number of elements. The term meta-cell is used to describe various subsets with a common name. In other words, there can be an arbitrary number of triangles in this cell complex attached to the innermost vertex.
Figure 1.7 presents the complex topology of a cuboid cell complex. The rectangle in the figure marks the main cell (5) under consideration. As can be seen, the number of attached cells is constant inside the space. The topology of the cell complex can thereby be used as a globally known property.