The previous sections introduced combinatorial concepts for CW-complex representations and abstract classification mechanisms to manage scientific data. Compared to the theory of CW-complexes, this section focuses more on the details of algebraic properties of linear mappings by a procedure to associate a sequence of Abelian groups or modules with, e.g., a topological space. Only a few concepts are introduced in this section [55,22], because of the fact that computational topology [56,19] is a complex and emerging part of scientific computing in its own right.
The motivation for this section is to retain the structure of geometrical objects and even physical field approximations for computational mechanisms, because the recovery of lost structural information of objects has proven to be a very complex and difficult tasks.
To use the elements of a dimension of a cell complex, e.g., all edges,
in a computational manner, a mapping of the ![]() -cells onto an
algebraic structure is needed. An algebraic representation of the
assembly of cells with a given orientation is thereby made available.
Whereas the cell topology is concerned about the internal structure of
a given cell, the chain concept acts on certain
-cells onto an
algebraic structure is needed. An algebraic representation of the
assembly of cells with a given orientation is thereby made available.
Whereas the cell topology is concerned about the internal structure of
a given cell, the chain concept acts on certain ![]() -cells.
A formal definition for a
-cells.
A formal definition for a ![]() -chain (
-chain (![]() chain group) is given
by:
chain group) is given
by:
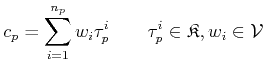 |
(1.24) |
| (1.25) |
Thus, two ![]() -chains can be added, or a
-chains can be added, or a ![]() -chain can be multiplied by
a scalar. In addition,
-chain can be multiplied by
a scalar. In addition, ![]() -chains support algebraic-topological
operations, including the boundary and coboundary operations. Based on
these concepts, a cell complex can be seen as a formal structure where
cells can be added, subtracted, and multiplied.
The cell complexes used in this work have a chain group in every
dimension. Homological concepts are applied here for the first time,
due to the fact that homology examines the connectivity between two
immediate dimensions. A structure-relating map between sets of chains
-chains support algebraic-topological
operations, including the boundary and coboundary operations. Based on
these concepts, a cell complex can be seen as a formal structure where
cells can be added, subtracted, and multiplied.
The cell complexes used in this work have a chain group in every
dimension. Homological concepts are applied here for the first time,
due to the fact that homology examines the connectivity between two
immediate dimensions. A structure-relating map between sets of chains
![]() is therefore introduced1.2.
is therefore introduced1.2.
![$\displaystyle \partial_p \tau_{p}^{i} = \sum_i (-1)^i [k_0, k_1, .., \tilde k_i, ...k_n]$](img256.png) |
(1.26) |
This can be seen as a boundary operator, that maps ![]() -chains onto the
-chains onto the
![]() -chains in their boundary.
It should not be confused with the geometric boundary of a point set.
This algebraic-topological operation defines a
-chains in their boundary.
It should not be confused with the geometric boundary of a point set.
This algebraic-topological operation defines a ![]() -chain in terms
of a
-chain in terms
of a ![]() -chain. It is compatible with the additive and the external
multiplicative structure of chains and builds a linear transformation:
-chain. It is compatible with the additive and the external
multiplicative structure of chains and builds a linear transformation:
 |
(1.27) |
Therefore, the boundary operator can be used linearly
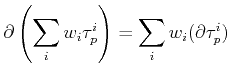 |
(1.28) |
which means that the boundary operator can be used separately for each
cell.
The cell complex properties can be easily calculated by means of
chains. 3-cells intersect on 2-cells or have an empty
intersection. This operation can be described by the boundary operator
![]() of the cell complex and the corresponding orientation
induced on them:
of the cell complex and the corresponding orientation
induced on them:
Figure 1.8 depicts two examples of 1-chains, 2-chains, and an example of the boundary operator. Applying the appropriate boundary operator to the 2-chain example read:
| (1.29) | |
| (1.30) |
Using the boundary operator on a sequence of chains of different dimensions, a chain complex is obtained:
| (1.31) |
| (1.32) |
Before the introduction of the concept of chains only the simple structure of a cell complex was available. The cell complex only contains the set of cells and their connectivity. The introduction of the chain concept provides the concept of an assembly of cells and the corresponding algebraic structure. Chains can be seen as mappings from oriented cells as part of a cell complex to another space. This definition establishes the algebraic access of computational methods to handle the concept of a cell complex.
In addition to cell complexes, scientific computing requires the
notation and access mechanisms to global quantities related to
macroscopic ![]() -dimensional space-time domains, introduced in Section
1.2. This collection of possible quantities,
which can be measured, can then be called a field, which permits the
modeling of these measurements as a field function that can be
integrated on arbitrary
-dimensional space-time domains, introduced in Section
1.2. This collection of possible quantities,
which can be measured, can then be called a field, which permits the
modeling of these measurements as a field function that can be
integrated on arbitrary ![]() -dimensional (sub)domains. An important fact
which has to be stated here is that all quantities which can be
measured are always attached to a finite region of space. A field
function can then be seen as the abstracted process of measurement of
this quantity [31,35].
The concept of cochains allows the association of numbers not only to
single cells, as chains do, but also to assemblies of cells. Briefly,
the necessary requirements are that this mapping is not only
orientation-dependent, but also linear with respect to the assembly of
cells, modeled by chains. A cochain representation is now the global
quantity association with subdomains of a cell complex, which can be
arbitrarily built to discretize a domain. Physical fields therefore
manifest on a linear assembly of cells. Based on cochains,
topological laws can be given a discrete representation.
-dimensional (sub)domains. An important fact
which has to be stated here is that all quantities which can be
measured are always attached to a finite region of space. A field
function can then be seen as the abstracted process of measurement of
this quantity [31,35].
The concept of cochains allows the association of numbers not only to
single cells, as chains do, but also to assemblies of cells. Briefly,
the necessary requirements are that this mapping is not only
orientation-dependent, but also linear with respect to the assembly of
cells, modeled by chains. A cochain representation is now the global
quantity association with subdomains of a cell complex, which can be
arbitrarily built to discretize a domain. Physical fields therefore
manifest on a linear assembly of cells. Based on cochains,
topological laws can be given a discrete representation.
The space of all linear mappings on ![]() is denoted by
is denoted by ![]() , where
the elements of
, where
the elements of ![]() are called cochains.
Cochains express a representation for fields over a discretized domain
are called cochains.
Cochains express a representation for fields over a discretized domain
![]() . Addition and multiplication by a scalar are defined
for the field functions and so for cochains.
To extend the expression possibilities, coboundaries of cochains are
introduced.
. Addition and multiplication by a scalar are defined
for the field functions and so for cochains.
To extend the expression possibilities, coboundaries of cochains are
introduced.
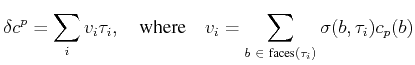 |
(1.33) |
| (1.34) |
| (1.35) |
Then, the following sequence with
![]() is generated:
is generated:
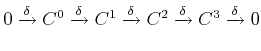 |
(1.36) |
The concepts of chains can also be used to characterize properties of
spaces, the homology and cohomology where it is only necessary to use
![]() . The algebraic structure of chains
is an important concept, e.g., to detect a
. The algebraic structure of chains
is an important concept, e.g., to detect a ![]() -dimensional hole that
is not the boundary of a
-dimensional hole that
is not the boundary of a ![]() -chain, which is called a
-chain, which is called a ![]() -cycle.
-cycle.
Figure 1.10 depicts the homology
of the three-dimensional chain complex with the respective images and
kernels, where the chain complex of
![]() is defined by
is defined by
![]() . As can be seen, the boundary operator expression yields
. As can be seen, the boundary operator expression yields
![]()
The first homology group [53] is the set of closed
1-chains (curves) in a space, modulo the closed 1-chains which are
also boundaries. In the remainder of this work the ring ![]() will be
will be
![]() or
or
![]() , in which case the modules
, in which case the modules ![]() are
vector spaces or Abelian groups, respectively, e.g., for
are
vector spaces or Abelian groups, respectively, e.g., for
![]() the chain complex is given by
the chain complex is given by
![]() or for the coefficient
group
or for the coefficient
group
![]() the following cochain complex
the following cochain complex
![]() .
.
To give an example, the first homology group is the set of closed
![]() -chains (curves) modulo the closed
-chains (curves) modulo the closed ![]() -chains which are also
boundaries.
This group is denoted
-chains which are also
boundaries.
This group is denoted
![]() , where
, where ![]() are cycles or closed
1-chains and
are cycles or closed
1-chains and ![]() are
are ![]() -boundaries. Another example is given in
Figure 1.11.
-boundaries. Another example is given in
Figure 1.11.
The concepts of chains and cochains coincide on finite complexes
[55]. Geometrically, however, ![]() and
and ![]() are
distinct [25] despite an isomorphism. An element of
are
distinct [25] despite an isomorphism. An element of
![]() is a formal sum of
is a formal sum of ![]() -cells, where an element of
-cells, where an element of ![]() is a
linear function that maps elements of
is a
linear function that maps elements of ![]() into a field. Chains are
dimensionless multiplicities, whereas those associated with cochains
are physical quantities [35]. The extension of
cochains from single cell weights to quantities associated with
assemblies of cells is not trivial and makes cochains very different
from chains, even on finite cell complexes. Nevertheless, there is an
important duality between
into a field. Chains are
dimensionless multiplicities, whereas those associated with cochains
are physical quantities [35]. The extension of
cochains from single cell weights to quantities associated with
assemblies of cells is not trivial and makes cochains very different
from chains, even on finite cell complexes. Nevertheless, there is an
important duality between ![]() -chains and
-chains and ![]() -cochains.
-cochains.
For a chain
![]() and a cochain
and a cochain
![]() , the integral of
, the integral of ![]() over
over
![]() is denoted by
is denoted by
![]() , and integration can be regarded
as a mapping, where
, and integration can be regarded
as a mapping, where ![]() represents the corresponding dimension:
represents the corresponding dimension:
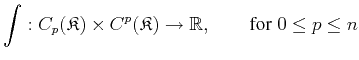 |
(1.37) |
Integration in the context of cochains is a linear operation: given
![]() and
and
![]() , reads
, reads
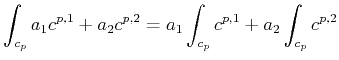 |
(1.38) |
Reversing the orientation of a chain means that integrals over that chain acquire the opposite sign
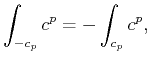 |
(1.39) |
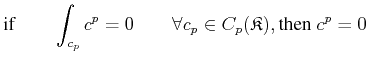 |
(1.40) |
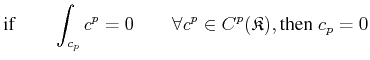 |
(1.41) |