1.6 Fiber Bundles and Chains/Cochains

This section combines the fiber bundle concepts and the computational topological concepts. The fiber bundle approach and the separation properties related to a base space offers a distinct modularization for application development for scientific computing. A modular system of software components is directly induced which always communicates over a formal interface, the preimage property. Likewise, the concept of chains transforms the properties of a cell complex directly to a computationally manageable algebraic structure. The final objective is to introduce operators that can be formulated generically, independently from all dimensional attributes. First, the tangent bundle and cotangent bundle concept is illustrated in Figure 1.16.

Figure 1.16: The identification of the concept of fiber bundles and the chain and cochain concept as dual spaces.

Then, the approach of a fiber bundle data model, where a discrete representation of a manifold is modeled by a CW-complex and the corresponding $X^{(p)}$ spaces, is given. These subspaces are modeled by separate base spaces, where a fiber describes the relationship to the remaining $X^{(m)}$ spaces, with $p!=m$ . The base space of the original problem is thereby constructed from these intrinsic relationship fiber bundles on the skeletons. An example is sketched in Figure 1.17, where a three-dimensional cell complex is depicted. Here, the vertex-on-cell and cell-on-vertex information is stored within the respective fiber spaces.

Figure 1.17: A representation of the intrinsic fiber bundles of the respective skeleton base spaces.

Related to this formulation of the fiber bundle concept, the chain concept uses the following concepts, where ${\ensuremath{\mathfrak{K}}}$ represents an arbitrary cell complex, as given in Section 1.4:

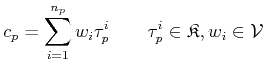$$c_p = \sum_{i=1}^{n_p}w_i \ensuremath{\tau_{p}^{i}} \quad \quad \... ...au_{p}^{i}} \in {\ensuremath{\mathfrak{K}}}, w_i \in {\ensuremath{\mathcal{V}}}$$ (1.50)

So a chain can be described by the intrinsic relationship fiber bundle of a $p$ -skeleton, whereas the $\ensuremath{\tau_{p}^{i}}$ part is mapped to a linear form within ${\ensuremath{\mathcal{T}}}_p$ / ${\ensuremath{\mathcal{T}}}_p{**}$ . The additional weight property is normally degenerate, which means that only the $\mathbb{Z}_2$ information is stored, e.g., only storing the cells of interest. These concepts can then be used in combination by the following identifications:

• Cell identification: this is the linear form on ${\ensuremath{\mathcal{T}}}_p{*}$ , here represented as $\ensuremath{\tau_{p}^{i}}$ , an element of the $n$ -skeleton.
• Incidence information: inherent fiber space property of the corresponding skeleton (not directly visible in the definition).
• Weight concepts (optional) with $w_i$ : an additional inherent fiber space property.

The only difference for the cochain concept is the space under consideration for the linear form, in this case the linear form on ${\ensuremath{\mathcal{T}}}_p$ . Then the linear forms on ${\ensuremath{\mathcal{T}}}_p$ and the linear forms on ${\ensuremath{\mathcal{T}}}_p^{*}$ , which are identified by multivectors and $p$ -forms, can be transfered to the algebraic bodies of chain and cochains complexes. The formal duality between vectors and covectors is also transfered to the duality between chains and cochains $\langle c_p, c^p \rangle$ .