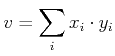Subsections

• 4.2.1 Object-Orientation Programming
• 4.2.2 Functional Programming
• 4.2.3 Generic Programming
• 4.2.4 Meta-Programming

4.2 Evolution of Programming Paradigms

The data model introduced in the last section shows that several tasks in the development of scientific application inherently require different programming paradigms by definition to model the underlying issues best.

In scientific computing there is a multitude of software tools available which provide methods and libraries for the solution of very specific problems. It is clear that such tools impose restrictions in various ways. The quest for highly reusable software components is still ongoing and demands different programming paradigms for an efficient realization.

A software component is reusable if it can be used beyond its initial use within a single application or group of applications without modification. The programming paradigms which are most widely used and implemented by various programming languages are:

• Imperative programming
• Object-oriented programming (OO)
• Functional programming (FP)
• Generic programming (GP)
• Meta-programming (MP)

These various paradigms were developed to cope with the important issue of enabling an efficient transformation of algorithms and concepts into code. One of the main issues is related to the given code reusability thereby identifying the concepts of monomorphic and polymorphic programming, one of the basic concepts for code reuse and orthogonal program development. Classical languages, such as different types of assembler or C, use a straight-forward monomorphic programming style based on the imperative programming paradigm. In the field of scientific computing, only one- and two-dimensional data structures were initially used to develop applications, due to the limitations of computer resources. The imperative programming paradigm was sufficient for this type of task. Code which is developed this way supports only single data types and cannot be reused at all.

With the improvement of computer hardware and the rise of the object-oriented programming paradigm, the shift to more complex data models was possible. Modern high-level languages such as C++ or Java [6] implement means for polymorphic programming which make code reuse possible, e.g., by inheritance. Whereas several new programming languages such as Ruby [83] and other derivatives do not bother the user with the data types and therefore offer various automatically casted types, statically typed programming languages such as C, C++, or Java offer different strategies. Implications to application development can be observed clearly by studying the evolution of the object-oriented paradigm from imperative programming. The object-oriented programming paradigm has significantly eased the software development of complex tasks, due to the decomposition of problems into modular entities. It allows the specification of class hierarchies with its virtual class polymorphism (subtyping polymorphism), which has been a major enhancement for many different types of applications. But another important goal in the field of scientific computing, orthogonal libraries, cannot be achieved easily by this paradigm [39]. A simple example for an orthogonal library is a software component which is completely exchangeable, e.g., a sorting algorithm for different data structures. An inherent property of this paradigm is the divergence of generality and specialization [84,85,86].

Thus the object-oriented programming paradigm is pushed to its limits by the various conceptual requirements in the field of scientific computing, due to problems with interface specifications, performance issues, and lack of orthogonality. Even though the trend of combining algorithms and data structures is able to provide generalized access to the data structures through objects, it is observable that the interfaces of these objects become more complex as more functionality is added. The intended generality often results in inefficiency of the programs, due to virtual function calls which have to be evaluated at run-time. Compiler optimizations such as inlining or loop-unrolling cannot be used efficiently, if at all. A lot of research has been carried out to circumvent these issues [87], but major problems arise in the details [88].

Modern paradigms, such as the generic programming paradigm [16,89], have the same major goals as object-oriented programming, such as reusability and orthogonality. However, the problem is tackled from a different point of view [90]. Together with meta-programming [45], generic programming accomplishes both a general solution for most application scenarios and highly specialized code parts for minor scenarios without sacrificing performance [91,92,93] due to partial specialization. The C++ language supports this paradigm with a type of polymorphism which is realized through template programming [94], static parametric polymorphism. Combining this type of polymorphism with meta-programming, the compiler can generate highly specialized code without adversely affecting orthogonality. This allows the programmer to focus on libraries which provide concise interfaces with an emphasis on orthogonality, as can already be found, e.g., in the the BGL [43]. Although Java has gained more functionality with respect to a multi-paradigm approach [95,96], its performance still cannot be compared to the run-time performance of C++ [5]. Another comparison of high-level languages as well as scripting languages is also available [97]. To give a brief overview, the simple problem of an inner product is used to demonstrate the discussed issues of employing several programming paradigms:

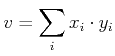$$v = \sum_i x_i \cdot y_i$$ (4.1)

A detailed performance comparison of the paradigms given here in C++ has been published [46].

4.2.1 Object-Orientation Programming

The object-oriented programming paradigm [98] introduced mechanisms required to obtain modular software design and reusability compared to universal accessibility of implementations by imperative programming. The main part of the object-oriented paradigm is related to the introduction of classes which cover basic properties of concepts to be implemented. Based on this description of properties, an object is created, which can be briefly explained by a self-governing unit of information which actively communicates with other objects. This is the main difference compared to a passive access as used in imperative programming languages. The concept of inheritance was introduced due to the fact that a particular concept, e.g., a mathematical $n$ -dimensional vector, cannot be described in its generality by a single class. By inheritance, semantically related concepts can be implemented in a class from which other classes can be derived, which should enable means of code reusability.

The first source snippet presents an implementation of the given problem in a fully object-oriented language, Java.

As can be observed, the connection between the implementation of the algorithm and the corresponding class Vector is very tight. All classes and methods which want to have access to this algorithm have to interface this class structure. Otherwise, the whole class has to be transfered to an interface, which has to be incorporated by other classes which want to use this algorithm. Either way this approach is intrusive, which means that the application of this algorithm requires a modification of the existing code. The object-oriented modeling, as presented, is strictly narrowed down for reusability within the class hierarchy. Despite the different aids for crossing this border, the inherent restriction in this example demonstrates that pure object-orientation does not lead to fully reusable components, due to the subtype bounds [77].

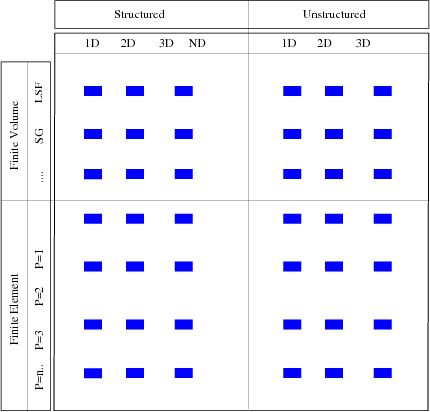
Another point of view can be presented if the amount of source code is reviewed which has to be implemented to develop an application in the field of scientific computing. For the case of a multi-discretization environment, different data structures have to be implemented, see Figure 4.2, where the top line gives a brief but incomplete overview of data structures required for the finite volume and the finite element methods. The vertical line presents different types of discretization schemes with the corresponding blocks, such as higher order finite elements, or different types of interpolation schemes for the finite volume method. For the object-oriented paradigm, all blue rectangles have to be implemented, e.g., finite volume with nonlinear interpolation functions.

Figure 4.2: Application design based on the object-oriented programming paradigm. Each of the inner blocks has to be implemented, resulting in an implementation effort of $\mathcal{O}(D \cdot A)$ , where $D$ stands for the number of data structures and $A$ for the number of algorithms.

For a general view of this paradigm, the implementation effort is estimated by $\mathcal{O}(D \cdot A)$ , where $D$ stands for the number of data structures and $A$ for the number of algorithms. Therefore, libraries for scientific computing, implemented by an object-oriented paradigm with a currently available run-time dispatch mechanism are not suitable for an efficient implementation, despite the performance penalty of object-oriented languages [46].

4.2.2 Functional Programming

A different type of programming paradigm is functional programming, where computation is treated as the evaluation of functions based on the following properties:

• Objects are provided only as constants or as expressions on objects.

• Functional programming avoids states of objects and mutable data. Loops therefore have to be replaced by recursion.

An important part of functional programming related to high performance is the delayed or lazy evaluation. This means that the moment in which a function is bound with some of its arguments can be separated from the one in which it is evaluated, thereby supporting the following techniques:

• Partial binding and partial evaluation, e.g., a binary function where one of the arguments is already bound to the function and only one parameter has to be specified to finally evaluate the function.

• Lambda expressions, based on the lambda calculus [99], use partial binding to define the expression $\lambda x y . f x y z$ , with the reserved prefix $\lambda$ , followed by the formal parameters, a dot, and the function definition.

• Currying, which creates unnamed lambda expressions automatically.

An implementation of the given problem is presented in the following source snippet using Haskell [7] as the host language. This programming paradigm, with the corresponding purely functional programming languages, such as Haskell, is currently widely used in the area of mathematical modeling. The static type mechanism and the generic mechanism, e.g., the availability of return type deduction, which goes beyond the capabilities of, e.g., C++, is an important feature and advantage of this language.

As can be seen, this representation of the algorithm is completely generic for all different types of input sequences, which can be added, folded, and transposed. The drawback of this mechanism is that it is already detached from the conventional programming style of C, Java, C++, or C# [3]. The functional modeling is fully reusable, because no assumptions about the used data types are made. Pure functional programming languages, such as Haskell, are completely polymorphic, concept-based programming languages. However, the issues with these languages are briefly explained by two drawbacks. First, the compiler has to do a lot of optimization work to reach the excellent performance of other programming languages such as Fortran or C++ [100,46,77]. Second, some tasks, such as input/output operations are inherently not functional and therefore difficult to model in such a programming languages. These parts of an application are always given by different states due to the fact that data sources, e.g., hard-disk or memory, are state-based. Functional programming does not support states from the beginning.

C++'s compile-time programming supports only the functional programming style. However, C++ is not a functional programming language, e.g., operators are not functions and cannot be used as first-class objects, but C++ allows the simulation of functional behavior. Functional programming therefore eases the specification of equations and offers extendable expressions, while retaining the functional dependence of formulae by lambda expressions (higher order functions). The C++ language uses additional libraries to support this paradigm [101,102,44].

4.2.3 Generic Programming

Generic programming denotes (object-oriented) programming methods based on the mechanism of parametric polymorphism of data structures and algorithms to obtain orthogonality, while avoiding the performance drawback of virtual function call costs [103] in C++. The generic programming paradigm thereby establishes homogeneous interfaces between algorithms and data structures without sub-typing polymorphism by an abstract access mechanism, the STL iterator concept. This concept specifies an abstract mechanism for accessing data structures in a concise way.

This algorithm can be used with any data structure which offers iterator access, whereby the most simple implementation of an iterator is a pointer to the data storage of a data structure. Based on the indirection of the iterator concept the overall implementation effort is greatly reduced. Problems arise in the details of the requirements of the iterators themselves, which are discussed in Appendix B. Nevertheless, an overall high performance can be obtained.

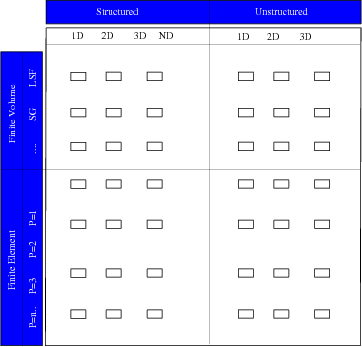
Figure 4.3: Application design based on the generic programming paradigm. Only the topmost and leftmost parts have to be implemented, which reduces the implementation effort to $\mathcal{O}(D + A)$.

In contrast to the object-oriented programming paradigm, the generic programming paradigm supports an orthogonal means for application design with the separation of algorithms and data structures, connected by the concept of iterators, or more generally, by traversal and abstract data accessors.

The implementation effort-combined with functional programming, which is greatly supported by the generic programming paradigm-is thereby reduced to $\mathcal{O}(D + A)$ and illustrated in Figure 4.3.

Generic modeling, together with the corresponding programming paradigm, supports both the derivation and state model mechanisms of object-oriented modeling, with the fully polymorphic support of functional programming. In other words, the generic paradigm supports the state-driven input/output with iterator or traversal concepts and the functional specification mechanism of functional programming languages. It can thereby be seen as the connector between the data sources and the specification. Not only can the implementation effort be reduced by several orders of magnitudes, but also be used to implement run-time code with the highest performance [46].

4.2.4 Meta-Programming

The paradigm of meta-programming can be briefly explained as writing a computer program that writes or manipulates other programs or themselves. For programming tasks which have to be repeated a great number of times, this paradigm can be used to obtain an efficient implementation [100,50].

Template meta-programming is a type of meta-programming in which the template (parametric polymorphism) system of the host language is used. The compiler uses these templates to generate new source code at compile-time. Template meta-programming is currently implemented by various programming languages, such as C++, Haskell, or D [4]. Here, only the implementation of this paradigm in C++ is used. C++ implements a Turing-complete template system, which means that any computation is expressible. In contrast to run-time programming, template meta-programming has non-mutuable variables and therefore requires the functional programming paradigm, most often used by recursion patterns.

The main advantages and disadvantages of this paradigm in C++ are:

• The generic programming paradigm is supported through template meta-programming by automatic code generation for various generic data structures or algorithms, e.g., the parametrization of data types for a simple container structure. Thereby truly generic code, facilitating code minimization and maintainability, is available.

• Due to the processing of the template system at compile-time, compilation can take a large amount of time. A careful selection of compile-time libraries and run-time libraries is therefore of utmost importance to implement large software projects. The most important benefit of this tradeoff is that the extended compile-times are used to obtain a highly efficient run-time code, sometimes superior even to Fortran implementations. See Section 7.4 for more details.

• One of the most severe drawbacks is the poor readability of template meta-programms. The operator overloading mechanism of C++ reduces this problem, but some operators cannot be overloaded, thus different language elements which cannot be easily identified as C++ source code are generated.

• Another drawback of template meta-programming is the reduced portability. However, especially the GNU compiler collection (GCC [104]) implementation of the C++ standard has significantly increased the availability of C++ on various platforms thereby reducing the portability problem in the future.

Together with generic programming, C++ template meta-programming enables another important concept for highly expressive code: domain-specific embedded languages.