



Next: Bibliography
Up: 4 Applied Concepts
Previous: Appendix B: STL Iterator Analysis
Appendix C: Cell Properties of Discretization Schemes
As introduced in Section 2,
the finite volume and finite element methods use different cell types for
their approximations. Finite volumes write the balance equations
in terms of global quantities, whereas finite elements, making use of
spread cells with spread boundaries, is forced to use field functions
defined locally over the whole domain. Despite this difference,
neither finite volume nor finite element discretize the operator
representing the local version of the balance equation. Instead they
both resort to a global version since a topological equation directly
applies to regions with finite extension. A detailed geometrical
analysis [33] based on the identification of the
weighting functions was given.
The weighted residual formulation of the finite element method starts
from the continuous formulation of a weighted domain:
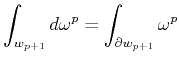 |
(13.1) |
The relationship between the two concepts, the continuous concept of
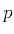 -differential forms (Section 1.7) and
the corresponding weighted domains, and the discrete concept related
to chains and cochains (Section
1.4) can be used to
algebraically handle the cells from a cell complex and the discrete
projection of a physical field. The weighted domain and the
-differential forms (Section 1.7) and
the corresponding weighted domains, and the discrete concept related
to chains and cochains (Section
1.4) can be used to
algebraically handle the cells from a cell complex and the discrete
projection of a physical field. The weighted domain and the 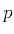 -form
are then directly related to the
-form
are then directly related to the 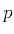 -chains and
-chains and 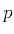 -cochains. When
-cochains. When
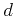 is used as a divergence operator, the following expression is
obtained in the discrete case:
is used as a divergence operator, the following expression is
obtained in the discrete case:
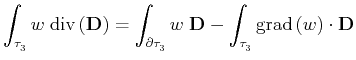 |
(13.2) |
where the 3-cell
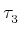 can be taken as the support of the
weight function
can be taken as the support of the
weight function 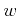 . With the expression for the boundary of a
weighted three-dimensional geometric object, the following formal
definition can be obtained:
. With the expression for the boundary of a
weighted three-dimensional geometric object, the following formal
definition can be obtained:
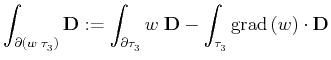 |
(13.3) |
where the
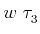 represents a weighted 3-cell. This
"boundary" includes actually an integral of the whole 3-cell
represents a weighted 3-cell. This
"boundary" includes actually an integral of the whole 3-cell
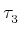 , and not only on
, and not only on
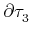 , except in the
particular case of a constant weight function on its supporting cell.
A corresponding interpretation of the weight function
, except in the
particular case of a constant weight function on its supporting cell.
A corresponding interpretation of the weight function 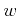 as a
continuous counterpart of a chain yields a concept called spread cell,
compared to a "crisp" cell, considered so far by a constant weight
function. If a weight function is constant on a cell and zero outside,
the second term of the equation vanishes and the finite element method
corresponds with a finite volume method. Due to the fact that these
spread cells overlap, this assembly of cells does not model the
concepts introduced for a consistent cell complex.
as a
continuous counterpart of a chain yields a concept called spread cell,
compared to a "crisp" cell, considered so far by a constant weight
function. If a weight function is constant on a cell and zero outside,
the second term of the equation vanishes and the finite element method
corresponds with a finite volume method. Due to the fact that these
spread cells overlap, this assembly of cells does not model the
concepts introduced for a consistent cell complex.
Figure C.1:
Geometrical interpretation of the basis functions for the (left) finite volume method and (right) for the finite element method. The finite volume method describes consistent crisp cells which can be interpreted as a cell complex, whereas the finite element method uses spread cells which do not conform with the properties of a consistent cell complex.
![\begin{figure}\begin{center}
\small\psfrag{x} [c]{$\ensuremath{\tau_{0}^{}}$}
...
...igures/fv_fe_ansatz_function.eps, width=0.8\textwidth}\end{center}\end{figure}](img967.png) |
Figure C.1 depicts the different
approaches of the finite volume and finite element method. The x-axis
is divided into one-dimensional cells, marked with vertical lines. The
finite volume method uses crisp cells which are aligned accordingly
with the dual complexes of the given cells of the underlying cell
complex. The finite element method uses spread cells which do not
build a consistent cell complex. In this example, each cell, depicted
by the basis function, is spread over two cells. From the point of
view of the dual complex, which is not used by the finite element
method, the cells extend beyond the area of a dual cell.
The important part of the integration by parts in the FE method can be
thereby explained with the necessity to operate with the boundary of
the FEM spread cells in order to express topological equations.




Next: Bibliography
Up: 4 Applied Concepts
Previous: 12. STL Iterator Analysis
R. Heinzl: Concepts for Scientific Computing
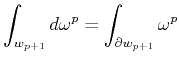
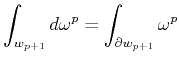
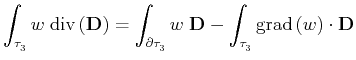
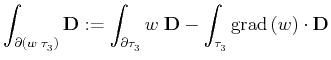
![\begin{figure}\begin{center}
\small\psfrag{x} [c]{$\ensuremath{\tau_{0}^{}}$}
...
...igures/fv_fe_ansatz_function.eps, width=0.8\textwidth}\end{center}\end{figure}](img967.png)