2. Numerical Discretization Schemes

An important step in handling partial differential equations is to use and develop stable, consistent, and accurate algebraic replacements where most of the global/continuous information of the original problem and more importantly, the inherent structure, are retained. Several methods are currently in use, such as the finite volume (FV), finite element (FE), and finite difference (FD) methods, each with specific approaches to discretization. Topological equations have an intrinsically discrete nature, compared to the constitutive parts of the field equations, which are the central issues in the construction of effective discretization schemes and the only place where recourse to local representations is fully justified. Numerical discretization schemes can be briefly represented as a model reduction, e.g.:

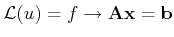$$\mathcal{L}(u) = {\ensuremath{f}} \rightarrow \ensuremath{\mathbf{A}} \ensuremath{\mathbf{x}} = \ensuremath{\mathbf{b}}$$ (2.1)

which transforms an infinite-dimensional operator equation into a finite-dimensional algebraic equation. Here it can already be seen that this is always accompanied by an inevitable loss of information due to the reduction of dimension. Briefly, the given discretization schemes address differently the task of replacing the partial differential equation system with algebraic ones. Therefore, generic discretization concepts, based on what has been called the reference discretization scheme [33,35], are introduced first. These concepts are then presented in the context of each of the other methods.

• The finite volume method is, with respect to the global and discrete formulation, based on topological laws, the most natural. The method is based on the approximation of conservation laws directly in its formulation and is therefore flux conserving by construction. The topological laws and time stepping procedures can be integrated easily.
• The finite element method can be seen as a remarkably flexible and general method for solving partial differential equations. Compared to the finite volume method, the spatial discretization can be much more arbitrary with fewer quality constraints. The continuous problem with an infinite amount of degrees of freedom is reformulated as an equivalent variational problem with a finite dimensional space. As described in the corresponding finite element section, this method is able to incorporate the constitutive relations appropriately. The incorporation of topological laws and time-dependent problems is more complex.

• The last scheme used in this work is the finite difference scheme, which addresses the problem of numerical analysis from a quite different approach when compared to the preceding two. Instead of using the conservation of the original problem (FV) or projecting the continuous problem into a finite dimensional space (FE), the finite difference method uses a finite difference approximation for the differential operators. Despite the fact that this method is simple and effective as well as easy to derive and implement, this approach gives an optimal solution to a different problem than the originally intended discretized field equation. This method is limited to structured grids or global cell complexes.