| Targets |
Ions species |
Implantation conditions |
Function type |
Ref. |
| amorphous silicon |
| silicon dioxide |
| silicon nitride |
|
| boron |
| phosphorus |
| arsenic |
| antimony |
|
|
Pearson |
[82] |
|
|
| Energy: 30 keV - 180 keV |
Dose:
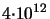 cm cm - -
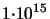 cm cm |
Tilt: 7
 , Rotation: 0 , Rotation: 0
 |
|
Joined half Gaussian with exponential tail |
[82] |
|
| boron |
BF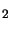 |
| arsenic |
| phosphorus |
| antimony |
| indium |
|
| Energy (boron): 10 keV - 160 keV |
Dose (boron):
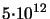 cm cm - -
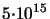 cm cm |
Energy (BF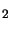 ): 5 keV - 60 keV ): 5 keV - 60 keV |
Dose (BF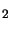 ): ):
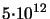 cm cm - -
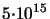 cm cm |
| Energy (phosphorus): 30 keV - 180 keV |
Dose (phosphorus):
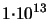 cm cm - -
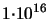 cm cm |
| Energy (arsenic): 20 keV - 160 keV |
Dose (arsenic):
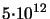 cm cm - -
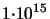 cm cm |
| Energy (antimony): 10 keV - 180 keV |
Dose (antimony):
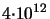 cm cm - -
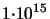 cm cm |
| Energy (indium): 30 keV - 180 keV |
Dose (indium):
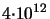 cm cm - -
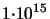 cm cm |
Tilt: 7
 , Rotation: 0 , Rotation: 0
 |
|
Pearson IV with exponential tail |
[84] |
| (100) silicon with |
10 nm - 120 nm SiO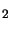 |
|
|
Tilt 0
 and 7 and 7
 |
|
Joined half Gaussian with exponential tail |
[83] |
| (111) silicon |
| silicon dioxide |
| silicon nitride |
|
|
| Energy (boron): 30 keV - 210 keV |
| Energy (arsenic): 30 keV - 400 keV |
Dose:
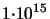 cm cm |
Tilt: 7
 |
|
Pearson |
[42] |
| (111) silicon |
| (100) silicon |
|
|
| Energy: 30 keV - 150 keV |
Dose:
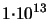 cm cm - -
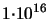 cm cm |
Tilt: 7
 |
|
Pearson |
[70] |
| (100) gallium-arsenide |
| (100) gallium-arsenide |
| with 50 nm nitride |
|
|
| Energy: 50 keV - 300 keV |
Dose:
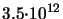 cm cm - -
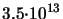 cm cm |
Tilt: 7
 , Rotation: 45 , Rotation: 45
 |
|
Pearson |
[86] |
|
|
| Energy (boron): 1 MeV - 7.1 MeV |
Dose (boron):
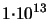 cm cm - -
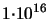 cm cm |
| Energy (phosphorus): 1 MeV - 5 MeV |
Dose (phosphorus):
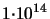 cm cm - -
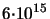 cm cm |
Tilt: 7
 |
|
Pearson |
[30] |
![]() defined for the one-dimensional case by
defined for the one-dimensional case by
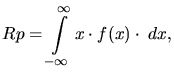
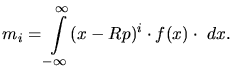
![]() and the straggling
and the straggling ![]() .
.

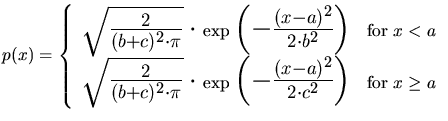
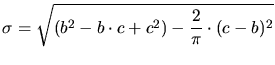
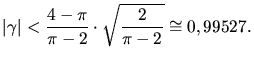
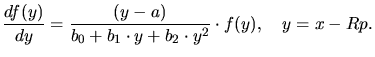
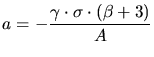
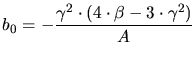
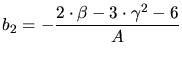
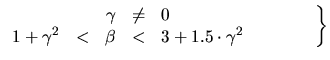 Type I
Type I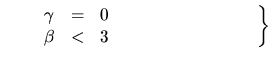 Type II
Type II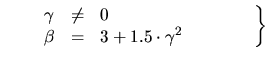 Type III
Type III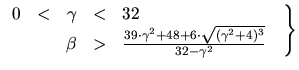 Type IV
Type IV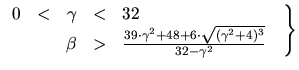 Type V
Type V Type VI
Type VI Type VII
Type VII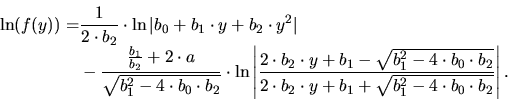
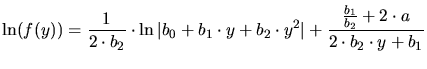
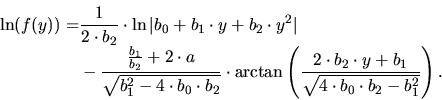
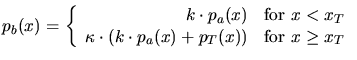
![$\displaystyle p_T(x) = k\cdot p_a(x_p)\cdot \exp\left[-\left( \frac{x-x_p}{L}\right) ^\alpha \right]$](img144.gif)
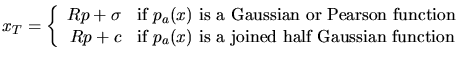
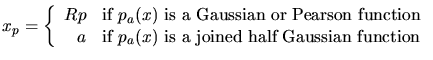
![]()
![]()
![]()
![]() Previous: 3.1 Analytical Method
Up: 3.1 Analytical Method
Next: 3.1.2 Two-Dimensional Point Response
Previous: 3.1 Analytical Method
Up: 3.1 Analytical Method
Next: 3.1.2 Two-Dimensional Point Response