previous up next contents Previous: 3.1.3 Three-Dimensional Point Response Up: 3.1 Analytical Method Next: 3.2 Point Response Interface

3.1.4 Multi-layered Structures

The point response functions described in Sec. 3.1.1 - Sec. 3.1.3 are only generally valid if the simulation domain consist just of one material which completely fills one half space. Normally the simulation domain consists of various materials which build up the transistor structure, for instance silicon, silicon dioxide, silicon nitride. In that case several point response functions (one for each material) have to be combined in a way that covering layers shift the point response profiles of layers lying underneath.

The numerical range scaling (NRS) technique proposed by Ryssel [67] has turned out to be a very efficient technique for the generation of multi-layer point response functions [30], [68]. By using this method a one-dimensional multi-layer point response function $ p(x)$ is designed as the sum of several single layer point response functions $ f_i(x)$ shifted by a scaling vector $ \delta _i$ and multiplied by a scaling factor $ \alpha _i$ which satisfies the normalization conditions (3.1).

$\displaystyle p(x) = \left\{ \begin{array}{r@{\hspace*{6mm}}rrcccl} f_1(x) &\te... ..._i \cdot f_i(x-\delta_i) &\text{for}& d_{i-1} &<& x &<& d_i \end{array} \right.$ (3.44)

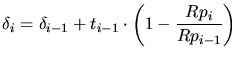$\displaystyle \delta_i = \delta_{i-1} + t_{i-1}\cdot \left(1-\frac{Rp_i}{Rp_{i-1}}\right)$ (3.45)

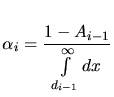$\displaystyle \alpha_i = \frac{1-A_{i-1}}{\int\limits_{d_{i-1}}^{\infty} dx}$ (3.46)

$\displaystyle A_i = \int\limits_{-\infty}^{d_{i}} f(x)\cdot \;dx = A_{i-1} + \int\limits_{d_{i-1}}^{d_{i}} \;dx\;\cdot \alpha_i \cdot f_i(x-\delta_i)$ (3.47)

$ t_i = d_i - d_{i-1}$ is the thickness of layer $ i$ and $ d_i$ denotes the coordinates of the material interfaces when the origin of the coordinate system is set to the surface of the simulation domain. An improved range scaling technique has been proposed in [87], where not only the projected range is scaled but also the straggling of the projected range. The modified straggling $ \tilde{\sigma_i}$ in layer $ i$ can be calculated by

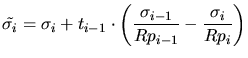$\displaystyle \tilde{\sigma_i} = \sigma_i +t_{i-1}\cdot \left( \frac{\sigma_{i-1}}{Rp_{i-1}} - \frac{\sigma_{i}}{Rp_{i}} \right)$ (3.48)

Higher dimensional multi-layer point response functions are modeled equivalently. This means that the vertical function and the moments of the lateral function are shifted by $ \delta _i$. Thereby it is assumed that each material is infinitely extended in the lateral directions. Arbitrary shaped simulation domains are handled by splitting the simulation domain into small vertical slices and by calculating a scaled point response function for each of these slices according to the material composition in the slice [55], [89]. (3.44) - (3.47) determine a different point response function for each slice and the total impurity concentration at position $ \vec{x}$ can be calculated by modifying (3.2) according to the existence of multiple point response functions.

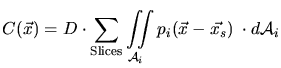$\displaystyle C(\vec{x}) = D\cdot \sum_{\text{Slices}} \iint\limits_{\mathcal{A}_i} p_i(\vec{x}-\vec{x_s}) \;\cdot d\mathcal{A}_i$ (3.49)

$ \mathcal{A}_i$ is the part of the surface area of the simulation domain related to slice $ i$.

previous up next contents Previous: 3.1.3 Three-Dimensional Point Response Up: 3.1 Analytical Method Next: 3.2 Point Response Interface

A. Hoessiger: Simulation of Ion Implantation for ULSI Technology